 |
 |
 |
 | Nonhyperbolic reflection moveout of 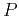 -waves:
An overview and comparison of reasons -waves:
An overview and comparison of reasons |  |
![[pdf]](icons/pdf.png) |
Next: Curved reflector beneath homogeneous
Up: CURVILINEAR REFLECTOR
Previous: CURVILINEAR REFLECTOR
If the reflector has the shape of a dipping plane beneath a homogeneous
isotropic medium, the reflection moveout in the dip direction is a hyperbola
(Levin, 1971)
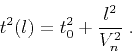 |
(53) |
Here
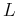 is the length of the zero-offset ray, and
is the length of the zero-offset ray, and 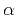 is the
reflector dip. Formula (53) is inaccurate if the
reflector is both dipping and curved. The Taylor series expansion for
moveout in this case has the form of equation
(22), with coefficients (Fomel, 1994)
is the
reflector dip. Formula (53) is inaccurate if the
reflector is both dipping and curved. The Taylor series expansion for
moveout in this case has the form of equation
(22), with coefficients (Fomel, 1994)
where
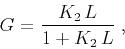 |
(58) |
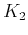 is the reflector curvature [defined by equation (61)]
at the reflection point of the zero-offset ray, and
is the reflector curvature [defined by equation (61)]
at the reflection point of the zero-offset ray, and 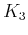 is the
third-order curvature [equation (62)]. If the reflector has
an explicit representation
is the
third-order curvature [equation (62)]. If the reflector has
an explicit representation 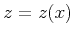 , then the parameters in equations
(56) and (57) are
, then the parameters in equations
(56) and (57) are
Keeping only three terms in the Taylor series leads to the approximation
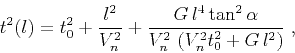 |
(63) |
where we included the denominator in the third term to ensure that the
traveltime behavior at large offsets satisfies the obvious limit
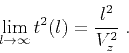 |
(64) |
As indicated by equation (61), the sign of the curvature 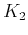 is
positive if the reflector is locally convex (i.e., an anticline-type).
The sign of
is
positive if the reflector is locally convex (i.e., an anticline-type).
The sign of 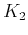 is negative for concave, syncline-type reflectors.
Therefore, the coefficient
is negative for concave, syncline-type reflectors.
Therefore, the coefficient 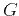 expressed by equation (58) and, likewise, the nonhyperbolic term in
(63) can take both positive and negative values. This means
that only for concave reflectors in homogeneous media do nonhyperbolic
moveouts resemble those in VTI and vertically heterogeneous media.
Convex surfaces produce nonhyperbolic moveout with the opposite sign.
Clearly, equation (63) is not accurate for strong
negative curvatures
expressed by equation (58) and, likewise, the nonhyperbolic term in
(63) can take both positive and negative values. This means
that only for concave reflectors in homogeneous media do nonhyperbolic
moveouts resemble those in VTI and vertically heterogeneous media.
Convex surfaces produce nonhyperbolic moveout with the opposite sign.
Clearly, equation (63) is not accurate for strong
negative curvatures
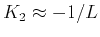 ,
which cause focusing of the
reflected rays and triplications of the reflection traveltimes.
,
which cause focusing of the
reflected rays and triplications of the reflection traveltimes.
In order to evaluate the accuracy of approximation (63), we
can compare it with the exact expression for a point diffractor, which
is formally a convex reflector with an
infinite curvature. The exact expression for normal moveout
in the present notation is
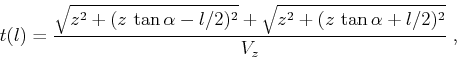 |
(65) |
where 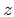 is the depth of the diffractor, and
is the depth of the diffractor, and 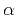 is the angle from
vertical of the
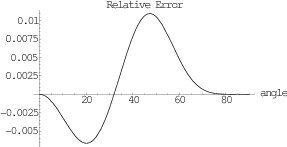
zero-offset ray. Figure 4 shows the relative error of
approximation (63) as a function of the ray angle for
offset
is the angle from
vertical of the
zero-offset ray. Figure 4 shows the relative error of
approximation (63) as a function of the ray angle for
offset 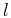 twice the diffractor depth
twice the diffractor depth 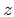 . The
maximum error of about 1% occurs at
. The
maximum error of about 1% occurs at
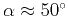 .
We can expect equation (63) to be even more accurate
for reflectors with smaller curvatures.
.
We can expect equation (63) to be even more accurate
for reflectors with smaller curvatures.
|
|---|
nmoerr
Figure 4. Relative error 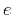 of the
nonhyperbolic moveout approximation (63) for a
point diffractor. The error corresponds to offset of the
nonhyperbolic moveout approximation (63) for a
point diffractor. The error corresponds to offset 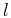 twice the diffractor depth twice the diffractor depth 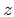 and is plotted against the angle from vertical and is plotted against the angle from vertical 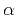 of
the zero-offset ray. of
the zero-offset ray.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[mathematica]](icons/mathematica.png)
|
|---|
 |
 |
 |
 | Nonhyperbolic reflection moveout of  -waves:
An overview and comparison of reasons -waves:
An overview and comparison of reasons |  |
![[pdf]](icons/pdf.png) |
Next: Curved reflector beneath homogeneous
Up: CURVILINEAR REFLECTOR
Previous: CURVILINEAR REFLECTOR
2013-03-03
