 |
 |
 |
 | Velocity analysis using 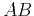 semblance
semblance |  |
![[pdf]](icons/pdf.png) |
Next: Appendix B: Automatic velocity
Up: Fomel: Velocity analysis using
Previous: Acknowledgments
In this appendix, I study the influence of noise on semblance
measures. Let us assume that the signal
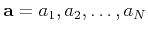 is composed of random independent
samples normally distributed with zero mean and
is composed of random independent
samples normally distributed with zero mean and 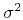 variance. In this case, the mathematical expectation for the semblance
measure (3) is
variance. In this case, the mathematical expectation for the semblance
measure (3) is
![$\displaystyle E\left[\beta^2(\mathbf{a})\right] = \frac{\displaystyle E\left[\l...
...\right]} {\displaystyle N\,\sum_{i=1}^{N} E\left[a_i^2\right]} = \frac{1}{N}\;.$](img35.png) |
(9) |
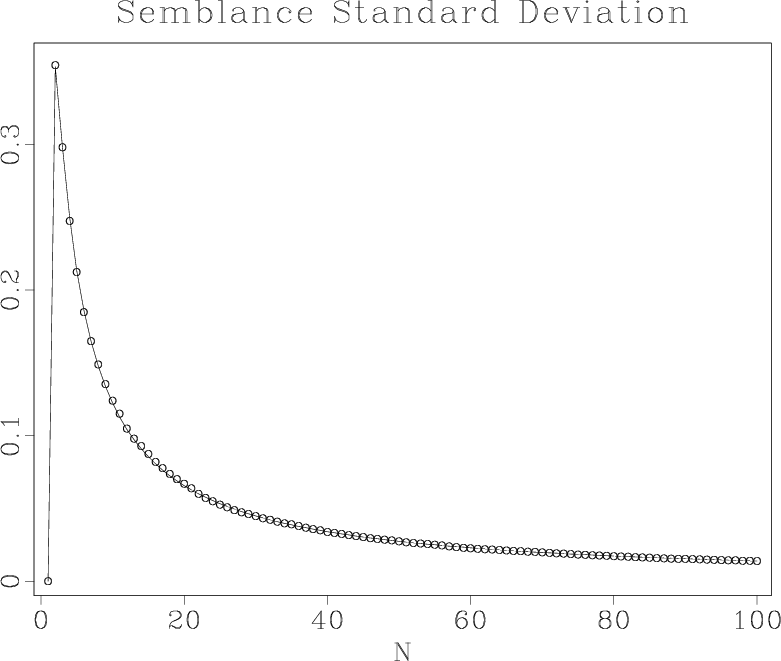
Correspondingly, the variance of the noise semblance is
Equations (A-1) and (A-2) show that both the
mathematical expectation and the standard deviation (the square root
of variance) of the random noise semblance decrease at the rate of
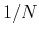 with the increase in the number of traces. To derive these
equations, I make an assumption that the terms in the numerator and
denominator are statistically independent. Rather than proving this
assumption mathematically, I test it by numerical experiments with
multiple random number realizations. Figure A-1
compares the theoretical prediction with experimental measurements
from 10,000 random realizations.
with the increase in the number of traces. To derive these
equations, I make an assumption that the terms in the numerator and
denominator are statistically independent. Rather than proving this
assumption mathematically, I test it by numerical experiments with
multiple random number realizations. Figure A-1
compares the theoretical prediction with experimental measurements
from 10,000 random realizations.
Applying similar analysis to the 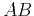 semblance (7), we deduce that
semblance (7), we deduce that
and
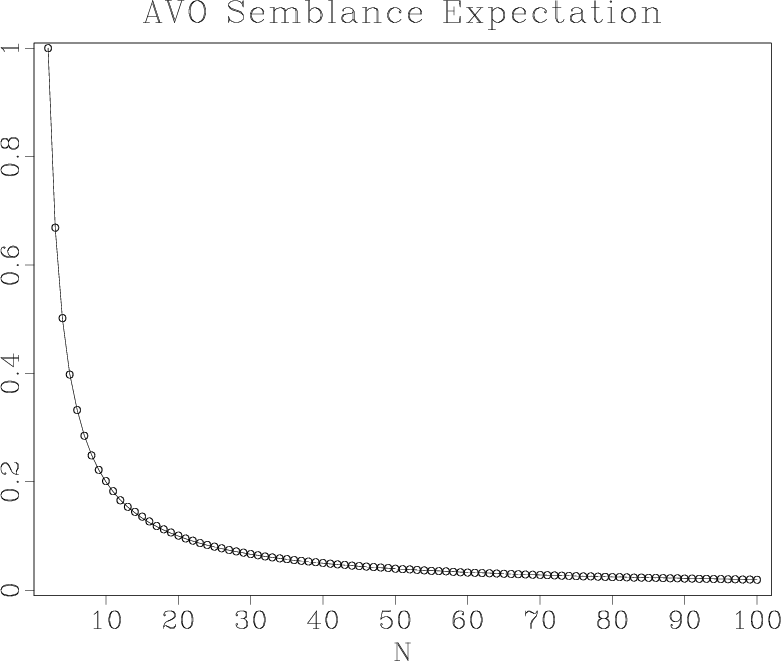
One can see that, in the case of the 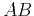 semblance, the
mathematical expectation and the standard deviation of the random
noise semblance decrease at the rate of
semblance, the
mathematical expectation and the standard deviation of the random
noise semblance decrease at the rate of 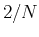 , twice higher than that
for the conventional semblance. Figure A-2 compares
the theoretical prediction with experimental measurements.
, twice higher than that
for the conventional semblance. Figure A-2 compares
the theoretical prediction with experimental measurements.
|
|---|
mean,vari
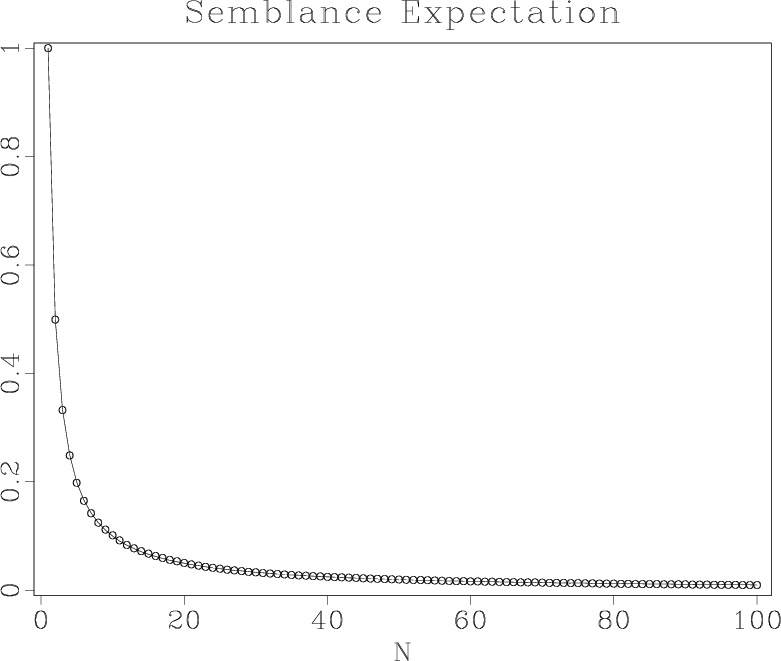
Figure 10. Mathematical expectation (a)
and standard deviation (b) of random-noise semblance as functions of
the number of traces 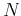 . Solid lines are theoretical curves, circles
are measurements from a numerical experiment.
. Solid lines are theoretical curves, circles
are measurements from a numerical experiment.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
amean,avari
Figure 11. Mathematical expectation (a) and standard deviation (b) of
random-noise 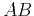 semblance as a function of the number of
traces
semblance as a function of the number of
traces 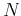 . Solid lines are theoretical curves, circles are
measurements from a numerical experiment.
. Solid lines are theoretical curves, circles are
measurements from a numerical experiment.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Velocity analysis using 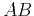 semblance
semblance |  |
![[pdf]](icons/pdf.png) |
Next: Appendix B: Automatic velocity
Up: Fomel: Velocity analysis using
Previous: Acknowledgments
2013-03-02
![]() is composed of random independent
samples normally distributed with zero mean and
is composed of random independent
samples normally distributed with zero mean and ![]() variance. In this case, the mathematical expectation for the semblance
measure (3) is
variance. In this case, the mathematical expectation for the semblance
measure (3) is
![]() semblance (7), we deduce that
semblance (7), we deduce that



