 |
 |
 |
 | Velocity analysis using 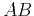 semblance
semblance |  |
![[pdf]](icons/pdf.png) |
Next: Sensitivity analysis of semblance
Up: Theory
Previous: Semblance as correlation
Suppose that the reference sequence has a trend
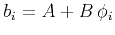 ,
where
,
where 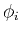 is a known function. The trend can be, for example, an
expression of the
is a known function. The trend can be, for example, an
expression of the 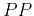 reflection coefficient in Shuey's approximation
(Shuey, 1985), where
reflection coefficient in Shuey's approximation
(Shuey, 1985), where 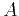 and
and 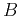 are the AVO intercept
and gradient,
are the AVO intercept
and gradient,
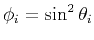 , and
, and 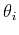 corresponds to
the reflection angle at trace
corresponds to
the reflection angle at trace 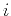 . In examples of this
paper, I use offset instead of angle. Relating offset and reflection
angle can be done either by using approximate equations of by ray
tracing once the velocity model is established.
. In examples of this
paper, I use offset instead of angle. Relating offset and reflection
angle can be done either by using approximate equations of by ray
tracing once the velocity model is established.
Estimating 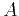 and
and 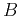 from least-square fitting of the trend amounts
to the minimization of
from least-square fitting of the trend amounts
to the minimization of
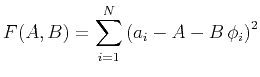 |
(4) |
Differentiating equation (4) with respect to 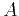 and
and 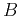 ,
setting the derivatives to zero, and solving the system of two linear
equations produces the well-known linear fit equations
,
setting the derivatives to zero, and solving the system of two linear
equations produces the well-known linear fit equations
Substituting the trend
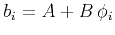 with
with 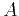 and
and 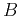 defined
from the least-squares equations (5) and (6) into the
correlation coefficient equation (1) and squaring the
result leads to equation
defined
from the least-squares equations (5) and (6) into the
correlation coefficient equation (1) and squaring the
result leads to equation
![$\displaystyle \boxed{ \alpha^2(\mathbf{a}) = \frac{\displaystyle 2\,\sum_{i=1}^...
...\left[\left(\sum_{i=1}^N \phi_i\right)^2 - N\,\sum_{i=1}^N \phi_i^2\right]}\;.}$](img29.png) |
(7) |
Equation (7) generalizes the semblance measure
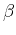 defined in equation (3) to a new measure
defined in equation (3) to a new measure 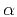 . In the absence of
a trend (when the numerator in equation (6) is zero),
. In the absence of
a trend (when the numerator in equation (6) is zero), 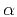 is
equivalent to
is
equivalent to 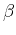 .
.
Sarkar et al. (2001) defined semblance using a
normalized least-squares objective
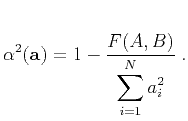 |
(8) |
Substituting equations (5) and (6) into (8)
is an alternative way of deriving equation (7). This is the
 semblance in terminology of
Sarkar et al. (2002,2001).
semblance in terminology of
Sarkar et al. (2002,2001).
 |
 |
 |
 | Velocity analysis using  semblance
semblance |  |
![[pdf]](icons/pdf.png) |
Next: Sensitivity analysis of semblance
Up: Theory
Previous: Semblance as correlation
2013-03-02
![]() ,
where
,
where ![]() is a known function. The trend can be, for example, an
expression of the
is a known function. The trend can be, for example, an
expression of the ![]() reflection coefficient in Shuey's approximation
(Shuey, 1985), where
reflection coefficient in Shuey's approximation
(Shuey, 1985), where ![]() and
and ![]() are the AVO intercept
and gradient,
are the AVO intercept
and gradient,
![]() , and
, and ![]() corresponds to
the reflection angle at trace
corresponds to
the reflection angle at trace ![]() . In examples of this
paper, I use offset instead of angle. Relating offset and reflection
angle can be done either by using approximate equations of by ray
tracing once the velocity model is established.
. In examples of this
paper, I use offset instead of angle. Relating offset and reflection
angle can be done either by using approximate equations of by ray
tracing once the velocity model is established.
![]() and
and ![]() from least-square fitting of the trend amounts
to the minimization of
from least-square fitting of the trend amounts
to the minimization of