 |
 |
 |
 | Velocity analysis using 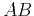 semblance
semblance |  |
![[pdf]](icons/pdf.png) |
Next: semblance: correlation with a
Up: Theory
Previous: Theory
The correlation coefficient 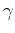 between two sequences of numbers
between two sequences of numbers
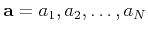 and
and
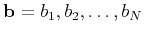 is defined as
is defined as
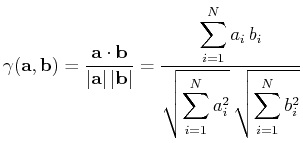 |
(1) |
The correlation coefficient is analogous to the cosine
of the angle between two vectors
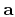 and
and
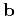 . It takes
values in the range from
. It takes
values in the range from 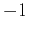 to
to 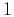 . Taking a correlation of a
sequence
. Taking a correlation of a
sequence
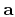 with a constant sequence
with a constant sequence
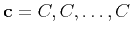 produces a measure
produces a measure 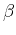 , defined as
, defined as
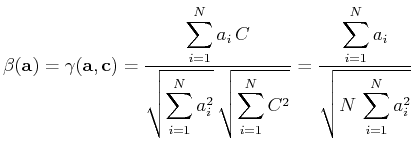 |
(2) |
Squaring the correlation with a constant yields the measure equivalent
to semblance
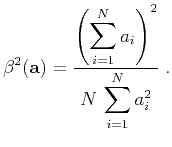 |
(3) |
Semblance is maximized when the sequence
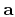 has a uniform
distribution. When seismic amplitude is uniformly distributed along a
moveout curve, the semblance of a horizontal slice through the gather
will be maximized when the event is flattened. This fact is the basis
of the conventional velocity analysis originally developed by
Taner and Koehler (1969). The approach fails, however, when the
amplitude variation is distinctly non-uniform.
has a uniform
distribution. When seismic amplitude is uniformly distributed along a
moveout curve, the semblance of a horizontal slice through the gather
will be maximized when the event is flattened. This fact is the basis
of the conventional velocity analysis originally developed by
Taner and Koehler (1969). The approach fails, however, when the
amplitude variation is distinctly non-uniform.
 |
 |
 |
 | Velocity analysis using 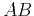 semblance
semblance |  |
![[pdf]](icons/pdf.png) |
Next: semblance: correlation with a
Up: Theory
Previous: Theory
2013-03-02
![]() between two sequences of numbers
between two sequences of numbers
![]() and
and
![]() is defined as
is defined as