|
|
|
|
Multidimensional autoregression |
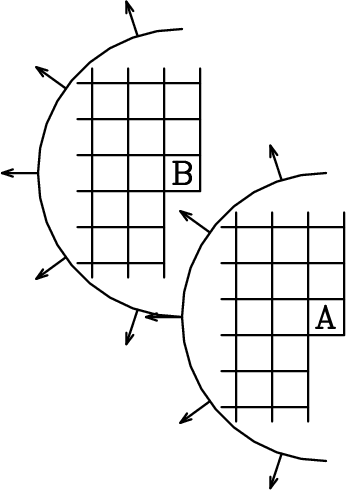
A well-known property (see FGDP or PVI) of a 1-D PEF is that its energy clusters immediately after the impulse at zero delay time. Applying this idea to the helix in Figure shows us that we can consider a 2-D PEF to be a small halfplane with an impulse along a side. These shapes are what we see here in Figure 2.
|
whitepruf
Figure 2. A 2-D whitening filter template, and itself lagged. At output locations ``A'' and ``B,'' the filter coefficient is constrained to be ``1''. When the semicircles are viewed as having infinite radius, the B filter is contained in the A filter. Because the output at A is orthogonal to all its inputs, which include all inputs of B, the output at A is orthogonal to the output of B. |
|
|---|---|
|
|
Figure 2 shows the input plane with a 2-D filter on top of it at two possible locations. The filter shape is a semidisk, which you should imagine being of infinitely large radius. Notice that semidisk A includes all the points in B. The output of disk A will be shown to be orthogonal to the output of disk B. Conventional least squares theory says that the coefficients of the filter are designed so that the output of the filter is orthogonal to each of the inputs to that filter (except for the input under the ``1,'' because any nonzero signal cannot be orthogonal to itself). Recall that if a given signal is orthogonal to each in a given group of signals, then the given signal is orthogonal to all linear combinations within that group. The output at B is a linear combination of members of its input group, which is included in the input group of A, which are already orthogonal to A. Therefore the output at B is orthogonal to the output at A. In summary,
| residual | fitting function | |
| output at A | each input to A | |
| output at A | each input to B | |
| output at A | linear combination of each input to B | |
| output at A | output at B |
The essential meaning is that a particular lag of the output autocorrelation function vanishes.
Study Figure 2 to see for what lags all the elements of the B filter are wholly contained in the A filter. These are the lags where we have shown the output autocorrelation to be vanishing. Notice another set of lags where we have proven nothing (where B is moved to the right of A). Autocorrelations are centrosymmetric, which means that the value at any lag is the same as the value at the negative of that lag, even in 2-D and 3-D where the lag is a vector quantity. Above we have shown that a halfplane of autocorrelation values vanishes. By the centrosymmetry, the other half must vanish too. Thus the autocorrelation of the PEF output is an impulse function, so its 2-D spectrum is white.
The helix tells us why the proper filter form is not a square with the ``1'' on the corner. Before I discovered the helix, I understood it another way (that I learned from John P. Burg): For a spectrum to be white, all nonzero autocorrelation lags must be zero-valued. If the filter were a quarter-plane, then the symmetry of autocorrelations would only give us vanishing in another quarter, so there would be two remaining quarter-planes where the autocorrelation was not zero.
Fundamentally, the white-output theorem requires a one-dimensional ordering to the values in a plane or volume. The filter must contain a halfplane of values so that symmetry gives the other half.
You will notice some nonuniqueness.
We could embed the helix
with a ![]() rotation
in the original physical application.
Besides the difference in side boundaries,
the 2-D PEF would have a different orientation.
Both PEFs should have an output that tends to whiteness as
the filter is enlarged.
It seems that we could design whitening autoregression filters
for
rotation
in the original physical application.
Besides the difference in side boundaries,
the 2-D PEF would have a different orientation.
Both PEFs should have an output that tends to whiteness as
the filter is enlarged.
It seems that we could design whitening autoregression filters
for ![]() rotations also,
and we could also design them for hexagonal coordinate systems.
In some physical applications,
you might find the nonuniqueness unsettling.
Does it mean the ``final solution'' is nonunique?
Usually not, or not seriously so.
Recall even in one dimension, the time reverse of a PEF
has the same spectrum as the original PEF.
When a PEF is used for regularizing a fitting application,
it is worth noticing that the quadratic form minimized
is the PEF times its adjoint so the phase drops out.
Likewise, a missing data restoration also amounts to minimizing
a quadratic form so the phase again drops out.
rotations also,
and we could also design them for hexagonal coordinate systems.
In some physical applications,
you might find the nonuniqueness unsettling.
Does it mean the ``final solution'' is nonunique?
Usually not, or not seriously so.
Recall even in one dimension, the time reverse of a PEF
has the same spectrum as the original PEF.
When a PEF is used for regularizing a fitting application,
it is worth noticing that the quadratic form minimized
is the PEF times its adjoint so the phase drops out.
Likewise, a missing data restoration also amounts to minimizing
a quadratic form so the phase again drops out.
|
|
|
|
Multidimensional autoregression |