|
|
|
|
Multidimensional autoregression |
Suppose the data set is a collection of seismograms
uniformly sampled in space.
In other words, the data is numbers in a ![]() -plane.
For example, the following filter
destroys any wavefront
aligned along the direction of a line containing both the ``+1''
and the ``
-plane.
For example, the following filter
destroys any wavefront
aligned along the direction of a line containing both the ``+1''
and the ``![]() ''.
''.
A two-dimensional filter that can be a dip-rejection filter like (22) or (23) is
Fitting the filter to two neighboring traces
that are identical but for a time shift, we see that
the filter coefficients
![]() should turn out to be
something like
should turn out to be
something like
![]() or
or
![]() ,
depending on the dip (stepout) of the data.
But if the two channels are not fully coherent, we expect to see
something like
,
depending on the dip (stepout) of the data.
But if the two channels are not fully coherent, we expect to see
something like
![]() or
or
![]() .
To find filters such as (24),
we adjust coefficients to minimize the power out
of filter shapes, as in
.
To find filters such as (24),
we adjust coefficients to minimize the power out
of filter shapes, as in
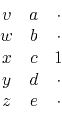 |
(26) |
With 1-dimensional filters,
we think mainly of power spectra,
and with 2-dimensional filters
we can think of temporal spectra and spatial spectra.
What is new, however,
is that in two dimensions we can think of dip spectra
(which is when a 2-dimensional spectrum has a particularly common form,
namely when energy organizes on radial lines in the
![]() -plane).
As a short (three-term) 1-dimensional filter can devour a sinusoid,
we have seen that simple 2-dimensional filters can devour
a small number of dips.
-plane).
As a short (three-term) 1-dimensional filter can devour a sinusoid,
we have seen that simple 2-dimensional filters can devour
a small number of dips.
|
|
|
|
Multidimensional autoregression |