|
|
|
|
Multidimensional autoregression |
Suppose we have many observations or many channels of ![]() so we label them
so we label them ![]() .
We can define a model
.
We can define a model ![]() as
as
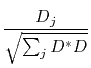 |
(27) |
Sometimes we have only a single signal ![]() but it is quite long.
Because the signal is long, the magnitude of its Fourier transform is rough,
so we smooth it over frequency, and denote it thus:
but it is quite long.
Because the signal is long, the magnitude of its Fourier transform is rough,
so we smooth it over frequency, and denote it thus:
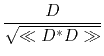 |
(28) |
These preliminary models are the most primative forms of deconvolved data.
They deal only with the amplitude spectrum.
Most deconvolutions involve also the phase.
The generally chosen phase is one with a causal filter.
A casual filter ![]() (vanishes before
(vanishes before ![]() )
with FT
)
with FT ![]() is chosen so that
is chosen so that ![]() is white.
Finding this filter is a serious undertaking,
normally done in a one-dimensional space.
Here, taking advantage of the helix, we do it in space of any number of dimensions.
is white.
Finding this filter is a serious undertaking,
normally done in a one-dimensional space.
Here, taking advantage of the helix, we do it in space of any number of dimensions.
For reasons explained later,
this is equivalent to minimizing the energy output of a filter beginning with a one,
![]() .
The inverse of this filter
.
The inverse of this filter ![]() is often called ``the impulse response'', or ``the source waveform''.
Whether it actually is a source waveform depends
on the physical setup as well as some mathematical assumptions we will learn.
is often called ``the impulse response'', or ``the source waveform''.
Whether it actually is a source waveform depends
on the physical setup as well as some mathematical assumptions we will learn.
|
|
|
|
Multidimensional autoregression |