 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: Null space and iterative
Up: KRYLOV SUBSPACE ITERATIVE METHODS
Previous: Method of random directions
Before we can understand why the conjugate-direction method is so fast,
we need to see why the
steepest-descent method
is so slow.
The process of selecting 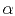 is called ``line search,''
but for a linear problem like the one we have chosen here,
we hardly recognize choosing
is called ``line search,''
but for a linear problem like the one we have chosen here,
we hardly recognize choosing 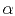 as searching a line.
A more graphic understanding of the whole process is possible
from considering a two-dimensional space,
where the vector of unknowns
as searching a line.
A more graphic understanding of the whole process is possible
from considering a two-dimensional space,
where the vector of unknowns 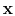 has just two components,
has just two components, 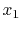 and
and 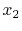 .
Then, the size of the residual vector
.
Then, the size of the residual vector
 can be
displayed with a contour plot in the plane of
can be
displayed with a contour plot in the plane of 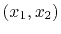 .
Figure 7
shows a contour plot of the penalty function
of
.
Figure 7
shows a contour plot of the penalty function
of
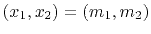 .
The gradient is perpendicular to the contours.
Contours and gradients are curved lines.
When we use the steepest-descent method, we start at a point
and compute the gradient direction at that point.
Then, we begin a straight-line descent in that direction.
The gradient direction curves away from our direction of travel,
but we continue on our straight line
until we have stopped descending and are about to ascend.
There we stop, compute another gradient vector,
turn in that direction, and descend along a new straight line.
The process repeats until we get to the bottom
or until we get tired.
.
The gradient is perpendicular to the contours.
Contours and gradients are curved lines.
When we use the steepest-descent method, we start at a point
and compute the gradient direction at that point.
Then, we begin a straight-line descent in that direction.
The gradient direction curves away from our direction of travel,
but we continue on our straight line
until we have stopped descending and are about to ascend.
There we stop, compute another gradient vector,
turn in that direction, and descend along a new straight line.
The process repeats until we get to the bottom
or until we get tired.
yunyue
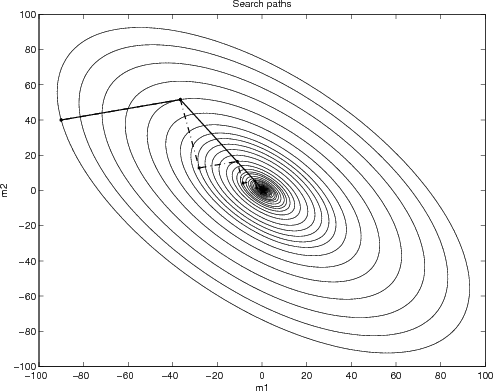
Figure 7.
Route of steepest descent (black)
and route of conjugate direction (light grey or red).
|
|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[matlab]](icons/matlab.png)
|
|---|
What could be wrong with such a direct strategy?
The difficulty is at the stopping locations.
These locations occur where the descent direction
becomes parallel to the contour lines.
(There the path becomes level.)
So, after each stop, we turn 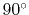 from parallel to perpendicular to the local contour line
for the next descent.
What if the final goal is at a
from parallel to perpendicular to the local contour line
for the next descent.
What if the final goal is at a  angle to our path?
A
angle to our path?
A  turn cannot be made.
Instead of moving like a rain drop down the centerline of a rain gutter,
we move along a fine-toothed zigzag path,
crossing and recrossing the centerline.
The gentler the slope of the rain gutter,
the finer the teeth on the zigzag path.
turn cannot be made.
Instead of moving like a rain drop down the centerline of a rain gutter,
we move along a fine-toothed zigzag path,
crossing and recrossing the centerline.
The gentler the slope of the rain gutter,
the finer the teeth on the zigzag path.
 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: Null space and iterative
Up: KRYLOV SUBSPACE ITERATIVE METHODS
Previous: Method of random directions
2014-12-01

![]() from parallel to perpendicular to the local contour line
for the next descent.
What if the final goal is at a
from parallel to perpendicular to the local contour line
for the next descent.
What if the final goal is at a ![]() angle to our path?
A
angle to our path?
A ![]() turn cannot be made.
Instead of moving like a rain drop down the centerline of a rain gutter,
we move along a fine-toothed zigzag path,
crossing and recrossing the centerline.
The gentler the slope of the rain gutter,
the finer the teeth on the zigzag path.
turn cannot be made.
Instead of moving like a rain drop down the centerline of a rain gutter,
we move along a fine-toothed zigzag path,
crossing and recrossing the centerline.
The gentler the slope of the rain gutter,
the finer the teeth on the zigzag path.