 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: The magical property of
Up: KRYLOV SUBSPACE ITERATIVE METHODS
Previous: Why steepest descent is
In applications where we fit
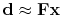 ,
there might exist a vector (or a family of vectors)
defined by the condition
,
there might exist a vector (or a family of vectors)
defined by the condition
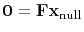 .
This family is called a null space.
For example, if the operator
.
This family is called a null space.
For example, if the operator 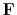 is a time derivative,
then the null space is the constant function;
if the operator is a second derivative,
then the null space has two components, a constant function
and a linear function, or combinations of both.
The null space is a family of model components that have no effect on the data.
is a time derivative,
then the null space is the constant function;
if the operator is a second derivative,
then the null space has two components, a constant function
and a linear function, or combinations of both.
The null space is a family of model components that have no effect on the data.
When we use the steepest-descent method,
we iteratively find solutions by this updating:
After we have iterated to convergence,
the gradient
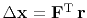 vanishes.
Adding any
vanishes.
Adding any
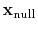 to
to 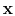 does not change the residual
does not change the residual
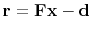 .
Because
.
Because 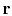 is unchanged,
is unchanged,
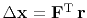 remains zero and
remains zero and
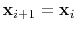 .
Thus, we conclude that any null space in the initial guess
.
Thus, we conclude that any null space in the initial guess 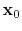 remains there unaffected by the gradient-descent process.
So, in the presense of null space,
the answer we get from an iterative method
depends on the starting guess.
Oops!
The analytic solution does not do any better.
It needs to deal with a singular matrix.
Existence of a null space destroys the uniqueness of any resulting model.
remains there unaffected by the gradient-descent process.
So, in the presense of null space,
the answer we get from an iterative method
depends on the starting guess.
Oops!
The analytic solution does not do any better.
It needs to deal with a singular matrix.
Existence of a null space destroys the uniqueness of any resulting model.
Linear algebra theory enables us to dig up the entire null space
should we so desire.
On the other hand, the computer demands might be vast.
Even the memory for holding the many 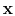 vectors could be prohibitive.
A much simpler and more practical goal
is to find out if the null space has any members,
and if so, to view some members.
To try to see a member of the null space,
we take two starting guesses,
and we run our iterative solver for each.
If the two solutions,
vectors could be prohibitive.
A much simpler and more practical goal
is to find out if the null space has any members,
and if so, to view some members.
To try to see a member of the null space,
we take two starting guesses,
and we run our iterative solver for each.
If the two solutions,
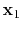 and
and 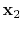 ,
are the same, there is no null space.
If the solutions differ, the difference
is a member of the null space.
Let us see why:
Suppose after iterating to minimum residual we find:
,
are the same, there is no null space.
If the solutions differ, the difference
is a member of the null space.
Let us see why:
Suppose after iterating to minimum residual we find:
We know that the residual squared is a convex quadratic function
of the unknown 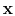 .
Mathematically that means the minimum value is unique,
so
.
Mathematically that means the minimum value is unique,
so
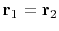 .
Subtracting,
we find
.
Subtracting,
we find
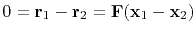 proving that
proving that
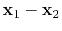 is a model in the null space.
Adding
is a model in the null space.
Adding
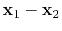 to any to any model
to any to any model 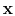 does not change the modeled data.
does not change the modeled data.
|
A practical way to learn about the existence of null spaces
and see samples is to try
gradient-descent methods
beginning from various different starting guesses.
|
``Did I fail to run my iterative solver long enough?'' is
a question you might have.
If two residuals from two starting solutions are not equal,
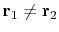 ,
then you should be running your solver through more iterations.
,
then you should be running your solver through more iterations.
|
If two different starting solutions
produce two different residuals,
then you did not run your solver through enough iterations.
|
 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: The magical property of
Up: KRYLOV SUBSPACE ITERATIVE METHODS
Previous: Why steepest descent is
2014-12-01
![]() vectors could be prohibitive.
A much simpler and more practical goal
is to find out if the null space has any members,
and if so, to view some members.
To try to see a member of the null space,
we take two starting guesses,
and we run our iterative solver for each.
If the two solutions,
vectors could be prohibitive.
A much simpler and more practical goal
is to find out if the null space has any members,
and if so, to view some members.
To try to see a member of the null space,
we take two starting guesses,
and we run our iterative solver for each.
If the two solutions,
![]() and
and ![]() ,
are the same, there is no null space.
If the solutions differ, the difference
is a member of the null space.
Let us see why:
Suppose after iterating to minimum residual we find:
,
are the same, there is no null space.
If the solutions differ, the difference
is a member of the null space.
Let us see why:
Suppose after iterating to minimum residual we find:
![]() ,
then you should be running your solver through more iterations.
,
then you should be running your solver through more iterations.