|
|
|
|
Model fitting by least squares |
Let us minimize the sum of the squares of the components
of the residual vector given by:
A contour plot is based on an altitude function of space.
The altitude is the dot product
![]() .
By finding the lowest altitude,
we are driving the residual vector
.
By finding the lowest altitude,
we are driving the residual vector ![]() as close as we can to zero.
If the residual vector
as close as we can to zero.
If the residual vector ![]() reaches zero, then we have solved
the simultaneous equations
reaches zero, then we have solved
the simultaneous equations
![]() .
In a two-dimensional world, the vector
.
In a two-dimensional world, the vector ![]() has two components,
has two components,
![]() .
A contour is a curve of constant
.
A contour is a curve of constant
![]() in
in ![]() -space.
These contours have a statistical interpretation as contours
of uncertainty in
-space.
These contours have a statistical interpretation as contours
of uncertainty in ![]() , with measurement errors in
, with measurement errors in ![]() .
.
Let us see how a random search-direction
can be used to reduce the residual
![]() .
Let
.
Let
![]() be an abstract vector
with the same number of components as the solution
be an abstract vector
with the same number of components as the solution ![]() ,
and let
,
and let
![]() contain arbitrary or random numbers.
We add an unknown quantity
contain arbitrary or random numbers.
We add an unknown quantity ![]() of vector
of vector
![]() to the vector
to the vector ![]() ,
and thereby create
,
and thereby create
![]() :
:
Next, we adjust ![]() to minimize the dot product:
to minimize the dot product:
![]()
A ``computation template'' for the method of random directions is:
A nice thing about the method of random directions is that you do not need to know the adjoint operator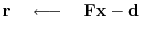
iterate {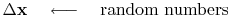

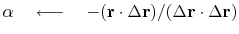
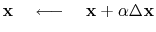
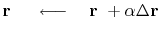
}
In practice, random directions are rarely used.
It is more common to use the gradient direction than a random direction.
Notice that a vector of the size of
![]() is:
is:
| (59) |
| (60) |
Starting from a model
![]() (which may be zero),
the following is a template of pseudocode for minimizing the residual
(which may be zero),
the following is a template of pseudocode for minimizing the residual
![]() by the steepest-descent method:
by the steepest-descent method:
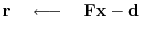
iterate {

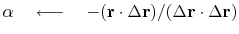
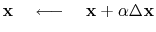
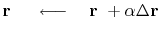
}
Good science and engineering is finding something unexpected.
Look for the unexpected both in data space and in model space.
In data space, you look at the residual ![]() .
In model space, you look at the residual projected there
.
In model space, you look at the residual projected there
![]() .
What does it mean?
It is simply
.
What does it mean?
It is simply ![]() ,
the changes you need to make to your model.
It means more in later chapters,
where the operator
,
the changes you need to make to your model.
It means more in later chapters,
where the operator ![]() is a column vector of operators
that are fighting with one another to grab the data.
is a column vector of operators
that are fighting with one another to grab the data.
|
|
|
|
Model fitting by least squares |