|
|
|
|
The helical coordinate |
|
|
|---|
|
diamond
Figure 1. Two-dimensional convolution as performed in one dimension by module helicon |
|
|
A surprising, indeed amazing, fact is that Figure 1 was not computed with a 2-dimensional convolution program. It was computed with a 1-dimensional computer program. It could have been done with anybody's 1-dimensional convolution program, either in the time domain or in the Fourier domain. This magical trick is done with the helical coordinate system.
A basic idea of filtering, be it in one dimension, two dimensions, or more, is that you have some filter coefficients and some sampled data; you pass the filter over the data; and at each location you find an output by crossmultiplying the filter coefficients times the underlying data and summing the products.
The helical coordinate system is much simpler than you might imagine. Ordinarily, a plane of data is thought of as a collection of columns, side by side. Instead, imagine the columns stored ``end-to-end,'' and then coiled around a cylinder. The concatenated columns make a helix. This arrangement is Fortran's way of storing 2-D arrays in 1-dimensional memory, and it is exactly what we need for this helical mapping. Seismologists sometimes use the word ``supertrace'' to describe a collection of seismograms stored end-to-end.
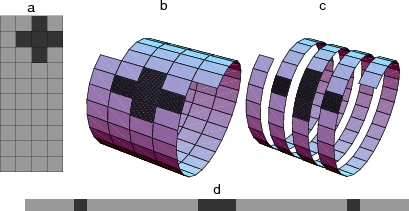
Figure 2 shows a helical mesh for 2-D data on a cylinder.
Darkened squares depict a 2-D filter
shaped like the Laplacian operator
![]() .
The input data, the filter, and the output data are all on helical meshes,
all of which could be unrolled into linear strips.
A compact 2-D filter like a Laplacian
on a helix is a sparse 1-D filter with long empty gaps.
.
The input data, the filter, and the output data are all on helical meshes,
all of which could be unrolled into linear strips.
A compact 2-D filter like a Laplacian
on a helix is a sparse 1-D filter with long empty gaps.
|
|---|
|
sergey-helix
Figure 2. Filtering on a helix. The same filter coefficients overlay the same data values if the 2-D coils are unwound into 1-D strips. (Mathematica drawing by Sergey Fomel) |
|
|
Because the values output from filtering can be computed in any order, we can slide the filter coil over the data coil in any direction. The order that you produce the outputs is irrelevant. You could compute the results in parallel. We could, however, slide the filter over the data in the screwing order that a nut passes over a bolt. The screw order is the same order that would be used if we were to unwind the coils into 1-dimensional strips and convolve the strips across one another. The same filter coefficients overlay the same data values if the 2-D coils are unwound into 1-D strips. The helix idea allows us to obtain the same convolution output in either of two ways, a 1-dimensional way or a 2-dimensional way. I used the 1-dimensional way to compute the obviously 2-dimensional result in Figure 1.
|
|
|
|
The helical coordinate |