 |
 |
 |
 | Fourier pseudo spectral method for attenuative simulation with fractional Laplacian |  |
![[pdf]](icons/pdf.png) |
Next: Fractional Laplacian
Up: Fourier pseudo spectral method
Previous: What is a pseudo-spectral
The Fourier transform of a function 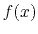 and the inverse are define respectively
and the inverse are define respectively
![$\displaystyle \tilde{f}(\omega)=F[f]=\int f(x)e^{-i\omega x}\mathrm{d}x$](img13.png) |
(4) |
and
![$\displaystyle f(x)=F^{-1}[f]=\frac{1}{2\pi}\int \tilde{f}(\omega)e^{i\omega x}\mathrm{d}\omega$](img14.png) |
(5) |
where 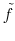 is the Fourier transform of
is the Fourier transform of 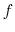 . In spatial dimension,
. In spatial dimension, 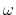 corresponds to the wavenumber
corresponds to the wavenumber 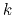 . Therefore we have
. Therefore we have
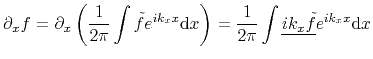 |
(6) |
and
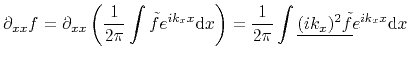 |
(7) |
The term
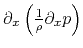 will be calculated by the following precedure:
will be calculated by the following precedure:
![\begin{displaymath}\begin{array}{rl} p\stackrel{F}{\longrightarrow}& \tilde{p}\\...
...{-1}[ik_xF[\frac{1}{\rho}F^{-1}[ik_x\tilde{p}]]] \\ \end{array}\end{displaymath}](img22.png) |
(8) |
Let us conduct a 2-D numerical simulation of acoustic wave equation with constant density. The equation is then
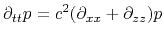 |
(9) |
Based upon Fourier transform for spatial axis, we know the right hand side of the above equation corresponds to
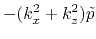 |
(10) |
Thus, we have the following time evolution
![$\displaystyle p^{n+1}=2p^n-p^{n-1}+\Delta t^2 c^2F^{-1}[-(k_x^2+k_z^2)F p^n]$](img25.png) |
(11) |
 |
 |
 |
 | Fourier pseudo spectral method for attenuative simulation with fractional Laplacian |  |
![[pdf]](icons/pdf.png) |
Next: Fractional Laplacian
Up: Fourier pseudo spectral method
Previous: What is a pseudo-spectral
2021-08-31
![]() and the inverse are define respectively
and the inverse are define respectively
![$\displaystyle \tilde{f}(\omega)=F[f]=\int f(x)e^{-i\omega x}\mathrm{d}x$](img13.png)
![$\displaystyle f(x)=F^{-1}[f]=\frac{1}{2\pi}\int \tilde{f}(\omega)e^{i\omega x}\mathrm{d}\omega$](img14.png)
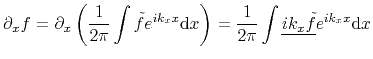
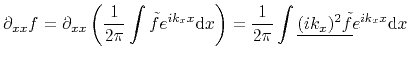
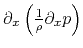 will be calculated by the following precedure:
will be calculated by the following precedure:
![\begin{displaymath}\begin{array}{rl} p\stackrel{F}{\longrightarrow}& \tilde{p}\\...
...{-1}[ik_xF[\frac{1}{\rho}F^{-1}[ik_x\tilde{p}]]] \\ \end{array}\end{displaymath}](img22.png)