Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators

Conclusions

We have proposed an alternative approach to simulate propagation of separated wave modes in general anisotropic media. The key idea is splitting the one-step wave mode separation into two cascaded steps based on the following observations: First, the Christoffel equation derived from the original elastic wave equation accurately represents the kinematics of all wave modes; Second, various coupled second-order wave equations can be derived from the Christoffel equation through similarity transformations. Third, wave mode separation can be achieved by projecting the original elastic wavefields onto the given mode's polarization directions, which are usually calculated based on the local material parameters using the Christoffel equation. Accordingly, we have derived the pseudo-pure-mode qP-wave equation by applying a similarity transformation aiming to project the elastic wavefield onto the wave vector, which is the isotropic references of qP-wave polarization for an anisotropic medium. The derived pseudo-pure-mode equations not only describe propagation of all wave modes but also implicitly achieve partial mode separation once the wavefield components are summed. As shown in the examples, the scalar pseudo-pure-mode qP-wave fields are dominated by qP-waves while the residual qS-waves are weaker in energy, because the projection deviations of qP-waves are generally far less than those of the qSV-waves. Synthetic example of Hess VTI model demonstrates successful application of the pseudo-pure-mode qP-wave equation to RTM for conventional seismic exploration. To completely remove the residual qS-waves, a filtering step has been proposed to correct the projection deviations resulting from the difference between polarization direction and its isotropic reference. In homogeneous media, it can be efficiently implemented by applying wavenumber domain filtering to each wavefield component. In heterogeneous media, nonstationary spatial filtering using pseudo-derivative operators are applied to finish the second step for wave mode separation. In a word, pseudo-pure-mode wave equations plus corrections of projection deviations provide us an efficient and flexible tool to simulate propagation of separated wave modes in anisotropic media.

In spite of the amplitude properties, this approach has some advantages over the classical solution combining elastic wavefield extrapolation and wave mode separation: First, the pseudo-pure-mode wave equations could be directly used for migration of seismic data recorded with single-component geophones without computationally expensive wave mode separation (as shown in the last example). Second, because partial wave mode separation is automatically achieved during wavefield extrapolation and the correction step to remove the residual qS-waves is optional depending on the strength of anisotropy, our approach provides better flexibilty for seismic modeling, migration and parameter inversion in practice; Third, computational cost is reduced at least one third for the 2D cases if the finite difference algorithms are used thanks to the simpler structure of pseudo-pure-mode wave equations (i.e., having no mixed derivative terms for VTI and vertically orthorhombic media). For the 3D TI media, computational cost is further reduced about one third because two instead of three equations are used to simulate wave propagation.

Unlike the pseudo-acoustic wave equations, pseudo-pure-mode wave equations have no approximation in kinematics and allow for 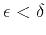$\epsilon<\delta$ provided that the stiffness tensor is positive-definite. Moreover, they provide a possibility to extract artifact-free separated wave mode during wavefield extrapolation. Although we focus on propagation of separated qP-waves using the pseudo-pure-mode qP-wave equation, our approach also works for qS-waves in TI media. This will be demonstrated in the second paper of this series.

Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators