|
|
|
|
Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |
Our final example shows application of the pseudo-pure-mode qP-wave equation (i.e., equation 22 in its 2D form)
to RTM of conventional seismic data representing mainly qP-wave energy using the synthetic data of
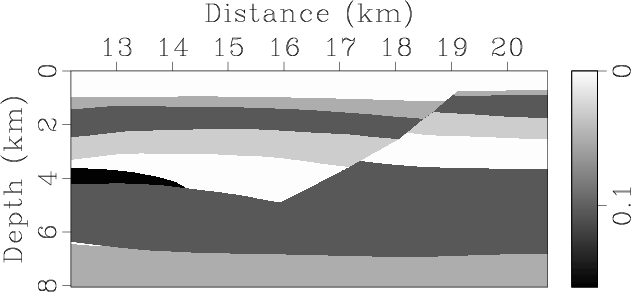
SEG/Hess VTI model (Figure 10).
In the original data set, there is no vertical velocity model for qSV-wave, namely ![]() .
For simplicity, we first get this parameter by setting
.
For simplicity, we first get this parameter by setting
![]() anywhere.
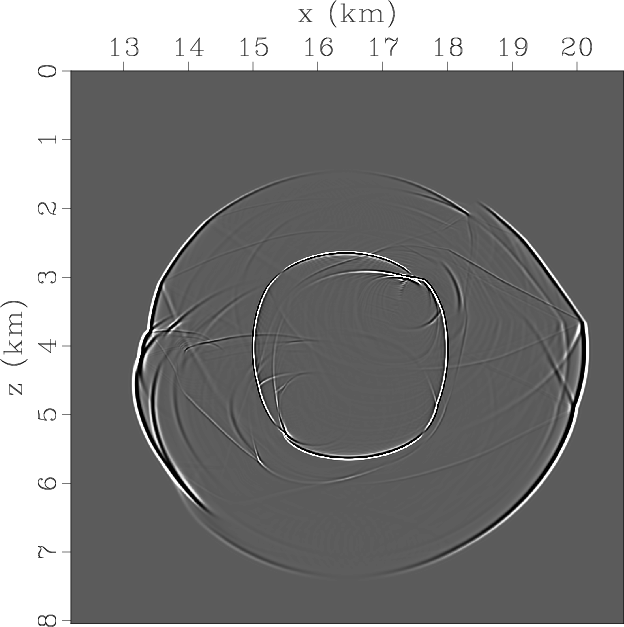
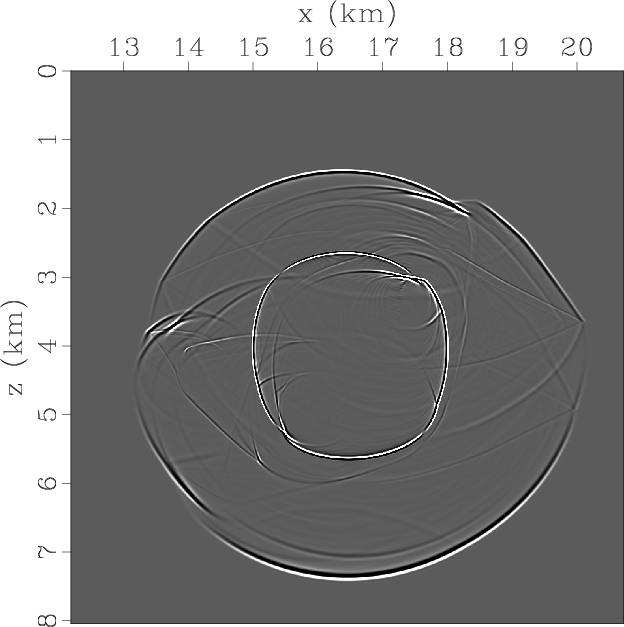
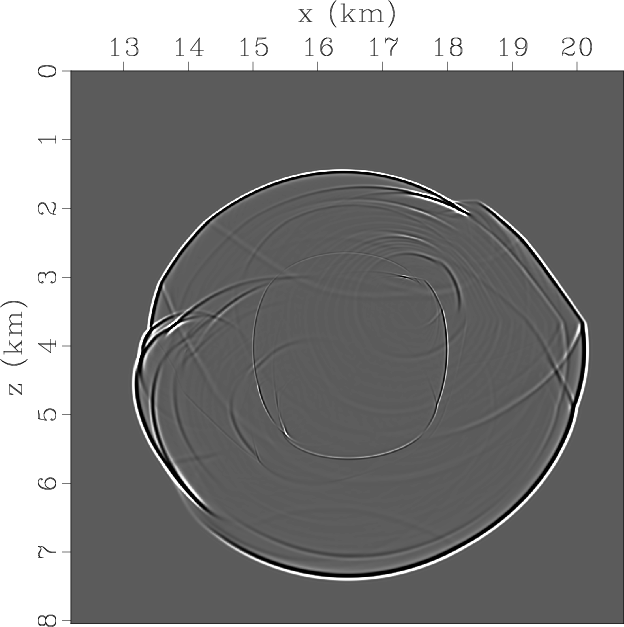
Figures 11a and 11b display the two components of the synthesized pseudo-pure-mode qP-wave fields,
in which the source is located at the center of the windowed region of the original models.
We observe that the summed wavefields (i.e., pseudo-pure-mode scalar qP-wave fields) contain quite weak
residual qSV-wave energy (Figure 11c).
For seismic imaging of qP-wave data, we try the finite nonzero
anywhere.
Figures 11a and 11b display the two components of the synthesized pseudo-pure-mode qP-wave fields,
in which the source is located at the center of the windowed region of the original models.
We observe that the summed wavefields (i.e., pseudo-pure-mode scalar qP-wave fields) contain quite weak
residual qSV-wave energy (Figure 11c).
For seismic imaging of qP-wave data, we try the finite nonzero ![]() scheme (Fletcher et al., 2009)
to suppress qSV-wave artifacts and enhance computation stability.
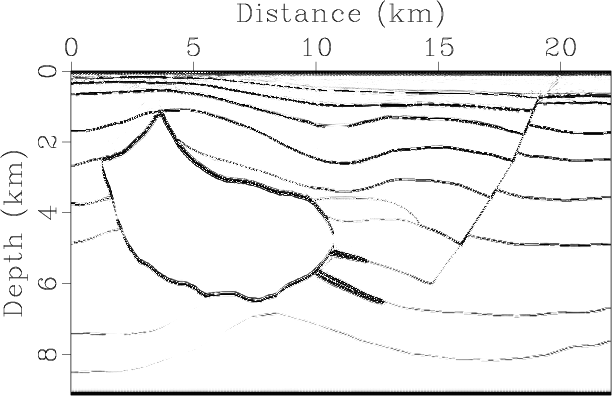
Thanks to superposition of multi-shot migrated data, we obtain a good RTM result (Figure 12)
using the common-shot gathers provided at http://software.seg.org, although spatial filtering
has not been used to remove the residual qSV-wave energy. This example shows that the proposed pseudo-pure-mode
qP-wave equation could be directly used for reverse-time migration of conventional single-component seismic data.
scheme (Fletcher et al., 2009)
to suppress qSV-wave artifacts and enhance computation stability.
Thanks to superposition of multi-shot migrated data, we obtain a good RTM result (Figure 12)
using the common-shot gathers provided at http://software.seg.org, although spatial filtering
has not been used to remove the residual qSV-wave energy. This example shows that the proposed pseudo-pure-mode
qP-wave equation could be directly used for reverse-time migration of conventional single-component seismic data.


|
|---|
|
hessvp0,hessepsilon,hessdelta
Figure 10. Part of SEG/Hess VTI model with parameters of (a) vertical qP-wave velocity, Thomsen coefficients (b) |
|
|
|
|---|
|
PseudoPurePx,PseudoPurePz,PseudoPureP
Figure 11. Synthesized wavefields using the pseudo-pure-mode qP-wave equation in SEG/Hess VTI model: The three snapshots are synthesized by fixing the ratio of |
|
|
|
|---|
|
hessrtm
Figure 12. RTM of Hess VTI model using the pseudo-pure-mode qP-wave equation with nonzero finite |
|
|
|
|
|
|
Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |