 |
 |
 |
 | Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Low-rank approximation solutions
Up: Cheng & Fomel: Anisotropic
Previous: Elastic wave mode separation
Wavefield decomposition aims achieving mode separation and vector decomposition simultaneously.
On the base of the Helmholtz theory and the theory of anisotropic wave mode separation via the Christoffell equation,
Zhang and McMechan (2010) develop a new solution to the problem of decomposing an elastic wavefield into P- and S-waves for
isotropic and VTI media. We summarize here only their results used for this study.
For isotropic media, the Helmholtz equations for the P-wave are transformed into the wavenumber-domain as,
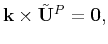 and and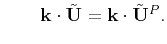 |
(7) |
From these equations, the vector decomposition equation of the separated P-wave is given by:
![$\displaystyle \tilde{\mathbf{U}}^P(\mathbf{k}) = \bar{\mathbf{k}}[\bar{\mathbf{k}}\cdot\tilde{\mathbf{U}(\mathbf{k})}].$](img49.png) |
(8) |
where
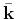 represents the normalized wave vector.
represents the normalized wave vector.
In a TI medium, equation 8 is extended to separate and decompose qP-wave by substituting
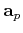 for
for
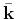 ,
,
![$\displaystyle \tilde{\mathbf{U}}^{qP}(\mathbf{k}) = \mathbf{a}_{p}(\mathbf{k})[\mathbf{a}_{p}(\mathbf{k})\cdot\tilde{\mathbf{U}}(\mathbf{k})].$](img52.png) |
(9) |
Similar equations
![$\displaystyle \tilde{\mathbf{U}}^{qSV}(\mathbf{k}) = \mathbf{a}_{sv}(\mathbf{k})[\mathbf{a}_{sv}(\mathbf{k})\cdot\tilde{\mathbf{U}}(\mathbf{k})],$](img53.png) |
(10) |
and
![$\displaystyle \tilde{\mathbf{U}}^{SH}(\mathbf{k}) = \mathbf{a}_{sh}(\mathbf{k})[\mathbf{a}_{sh}(\mathbf{k})\cdot\tilde{\mathbf{U}}(\mathbf{k})],$](img54.png) |
(11) |
are proposed to decompose qSV and SH waves using their respective polarization vectors.
Note that vector decomposition satisfies the linear superposition relation
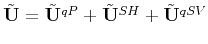 ,
and the separated wavefields are orthogonal to one another and have the same amplitude, phase, and physical units as the input wavefields.
,
and the separated wavefields are orthogonal to one another and have the same amplitude, phase, and physical units as the input wavefields.
 |
 |
 |
 | Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Low-rank approximation solutions
Up: Cheng & Fomel: Anisotropic
Previous: Elastic wave mode separation
2014-06-24
![]() for
for
![]() ,
,