 |
 |
 |
 | Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Elastic wave vector decomposition
Up: Cheng & Fomel: Anisotropic
Previous: Introduction
Using the Helmholtz decomposition theory (Aki and Richards, 1980; Morse and Feshbach, 1953),
a vector wavefield
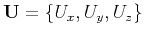 can be decomposed into
a curl-free P-wavefield and a divergence-free S-wavefield:
can be decomposed into
a curl-free P-wavefield and a divergence-free S-wavefield:
 . The P- and S-waves satisfy, respectively,
. The P- and S-waves satisfy, respectively,
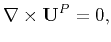 and and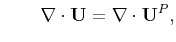 |
(1) |
and
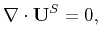 and and |
(2) |
These equations imply that the divergence and curl operations pass P- and S-wave modes respectively.
In the Fourier-domain, equivalent operations are expressed as follows:
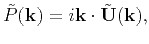 and and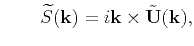 |
(3) |
where
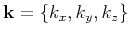 represents the wave vector and
represents the wave vector and
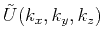 is the
3D wavefield in the wavenumber domain.
These operations essentially project the elastic wavefield onto the wave vector or its orthogonal directions,
thus separate P- and S-waves successfully.
In anisotropic media, however, qP- and qS-waves are not generally polarized parallel and perpendicular to the wave vector.
Dellinger and Etgen (1990) extended wave mode separation to anisotropic media with the following divergence-like and
curl-like operators in the wavenumber-domain,
is the
3D wavefield in the wavenumber domain.
These operations essentially project the elastic wavefield onto the wave vector or its orthogonal directions,
thus separate P- and S-waves successfully.
In anisotropic media, however, qP- and qS-waves are not generally polarized parallel and perpendicular to the wave vector.
Dellinger and Etgen (1990) extended wave mode separation to anisotropic media with the following divergence-like and
curl-like operators in the wavenumber-domain,
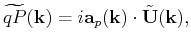 and and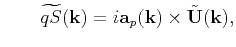 |
(4) |
where
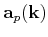 stands for the normalized polarization vector of qP wave in the wavenumber domain, calculated
from Christoffel equation.
Note that the second equation of equation 4 separates only the shear part of the
elastic wavefields, which contain the fast and low S-waves, i.e.,
stands for the normalized polarization vector of qP wave in the wavenumber domain, calculated
from Christoffel equation.
Note that the second equation of equation 4 separates only the shear part of the
elastic wavefields, which contain the fast and low S-waves, i.e., 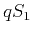 - and
- and 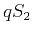 modes.
Unlike the well-behaved qP mode, the two qS modes do not consistently polarize as a function of the propagation direction (or wavenumber) and
thus cannot be designated as SV and SH waves, except in isotropic and TI media (Crampin, 1991; Zhang and McMechan, 2010; Dellinger, 1991; Winterstein, 1990).
In this paper, the approaches to separate and decompose qS-waves are restricted to TI anisotropy.
modes.
Unlike the well-behaved qP mode, the two qS modes do not consistently polarize as a function of the propagation direction (or wavenumber) and
thus cannot be designated as SV and SH waves, except in isotropic and TI media (Crampin, 1991; Zhang and McMechan, 2010; Dellinger, 1991; Winterstein, 1990).
In this paper, the approaches to separate and decompose qS-waves are restricted to TI anisotropy.
For TI media, one can separate scalar qSV and SH waves by projecting the
elastic wavefield onto their polarization directions using
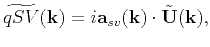 and and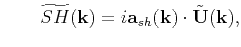 |
(5) |
where
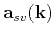 and
and
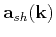 represent normalized polarization vectors of the qSV and SH waves, respectively.
For heterogeneous TI media, these operations can be expressed as nonstationary filtering in the space domain (Yan and Sava, 2009b).
In fact, the cost may become prohibitive in 3D because it is proportional to the number of grids in the model and the size of each filter (Yan and Sava, 2011).
represent normalized polarization vectors of the qSV and SH waves, respectively.
For heterogeneous TI media, these operations can be expressed as nonstationary filtering in the space domain (Yan and Sava, 2009b).
In fact, the cost may become prohibitive in 3D because it is proportional to the number of grids in the model and the size of each filter (Yan and Sava, 2011).
In general, we can determine polarization vectors by solving the Christoffel equation:
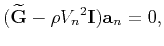 |
(6) |
where
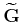 represents the Christoffel tensor in the Voigt notation with
represents the Christoffel tensor in the Voigt notation with
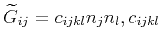 as the stiffness tensor, and
as the stiffness tensor, and
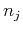 and
and 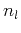 are the normalized wave vector components in
are the normalized wave vector components in 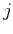 and
and 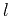 directions, with
directions, with
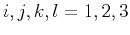 . The
parameter
. The
parameter
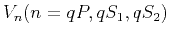 represents phase velocities of
represents phase velocities of 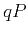 -,
-, 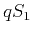 - and
- and 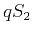 -wave modes.
The Christoffel equation poses a standard
-wave modes.
The Christoffel equation poses a standard  eigenvalue problem, the three eigenvalues of which correspond to phase
velocities of the three wave modes and the corresponding eigenvector
eigenvalue problem, the three eigenvalues of which correspond to phase
velocities of the three wave modes and the corresponding eigenvector
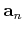 represents polarization direction of the given mode.
When shear singularities appear, the coincidence of the longitudinal and
transverse polarizations prevents us from
constructing 3D global operators to separate qSV and SH waves on the base of the Christoffel solution,
and the polarization discontinuity will cause the two modes to leak energy into each other
(Yan and Sava, 2009a; Zhang and McMechan, 2010; Dellinger, 1991; Yan and Sava, 2011).
Following Yan and Sava (2009a,2011), we mitigate the kiss singularity at
represents polarization direction of the given mode.
When shear singularities appear, the coincidence of the longitudinal and
transverse polarizations prevents us from
constructing 3D global operators to separate qSV and SH waves on the base of the Christoffel solution,
and the polarization discontinuity will cause the two modes to leak energy into each other
(Yan and Sava, 2009a; Zhang and McMechan, 2010; Dellinger, 1991; Yan and Sava, 2011).
Following Yan and Sava (2009a,2011), we mitigate the kiss singularity at
 in 3D TI media by using relative qP-qSV-SH mode
polarization orthogonality and scaling the polarizations of the qSV- and SH-waves by
in 3D TI media by using relative qP-qSV-SH mode
polarization orthogonality and scaling the polarizations of the qSV- and SH-waves by
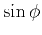 ,
with
,
with  being the polar angle.
being the polar angle.
 |
 |
 |
 | Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Elastic wave vector decomposition
Up: Cheng & Fomel: Anisotropic
Previous: Introduction
2014-06-24