 |
 |
 |
 | Fast time-to-depth conversion and interval velocity estimation in the case of weak lateral variations |  |
![[pdf]](icons/pdf.png) |
Next: Land field data example
Up: Examples
Previous: Linear sloth model
We further test the proposed method with another synthetic model that contains stronger velocity variations in both vertical and horizontal directions. In this model, the exact velocity is given by
 |
(23) |
where 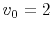
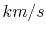 ,
, 
 , and
, and 
 . These parameters give 33-50
. These parameters give 33-50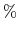 changes in horizontal velocity and a maximum of 60
changes in horizontal velocity and a maximum of 60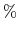 change in vertical velocity. The analytical solutions to time-to-depth conversion in this particular type of model were given by (Li and Fomel, 2015):
change in vertical velocity. The analytical solutions to time-to-depth conversion in this particular type of model were given by (Li and Fomel, 2015):
where
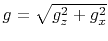 denotes the magnitude of the total gradient. It follows from equations 24 and 25 that
denotes the magnitude of the total gradient. It follows from equations 24 and 25 that
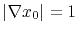 ,
,
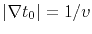 , and
, and
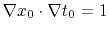 , which indicate that the geometrical spreading of image rays in this model is equal to one and the Dix velocity is equal to the interval velocity expressed in the time-domain coordinates
, which indicate that the geometrical spreading of image rays in this model is equal to one and the Dix velocity is equal to the interval velocity expressed in the time-domain coordinates 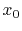 and
and 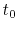 (equation 3). Nonetheless, the image rays still bend laterally because
(equation 3). Nonetheless, the image rays still bend laterally because 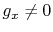 and will lead to distorted time-domain coordinates. The migration velocity squared
and will lead to distorted time-domain coordinates. The migration velocity squared 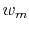 and its Dix-inverted counterpart
and its Dix-inverted counterpart 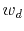 can also be derived analytically and are given by (Li and Fomel, 2015):
can also be derived analytically and are given by (Li and Fomel, 2015):
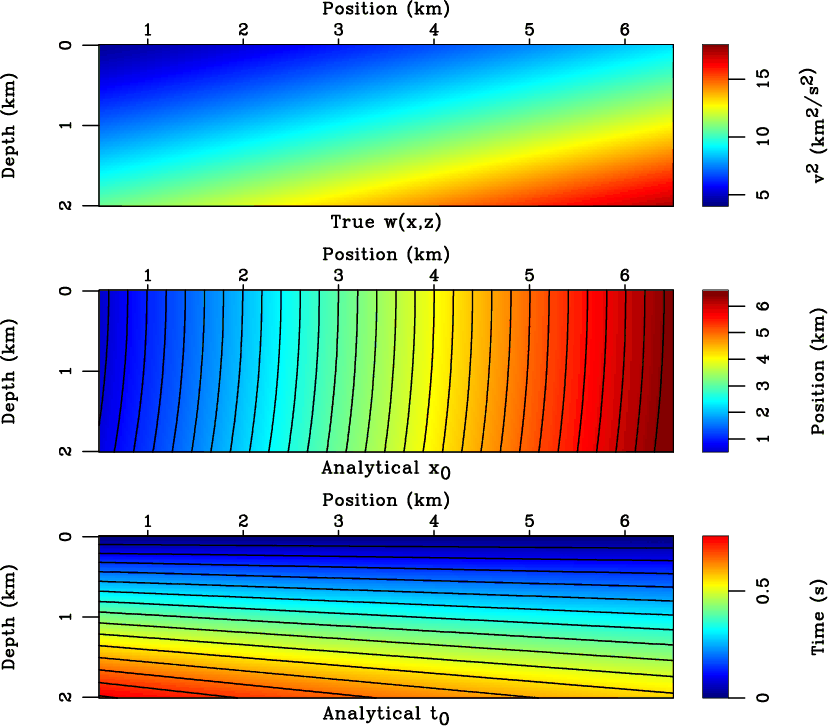
Figure 7 shows the true interval velocity of the model (equation 23), and the analytical 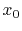 and
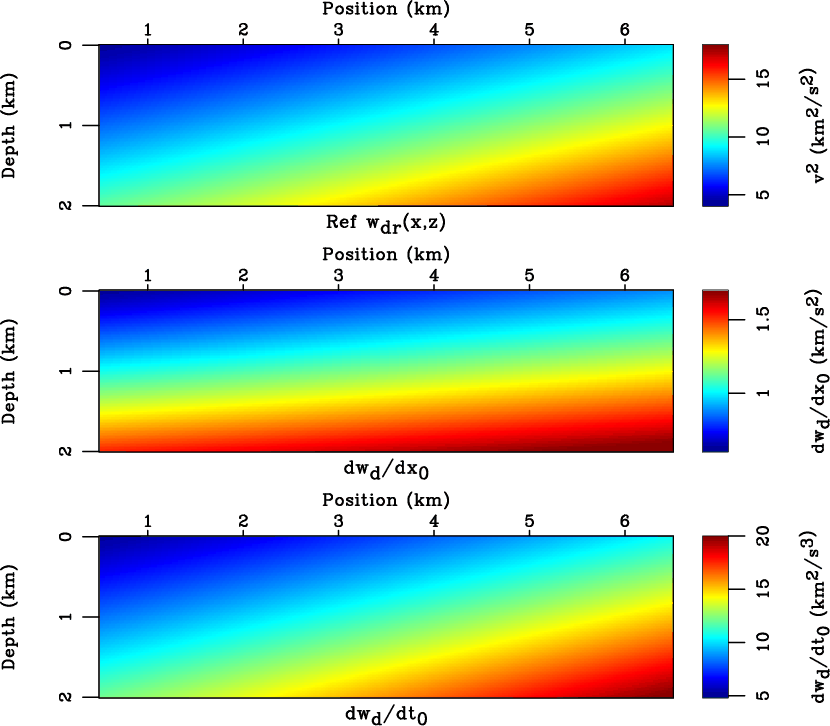
and 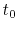 overlaid by the contours that show image rays and propagating image wavefront. Figure 8 shows other inputs for the proposed conversion method. Again, we arbitrarily choose the reference
overlaid by the contours that show image rays and propagating image wavefront. Figure 8 shows other inputs for the proposed conversion method. Again, we arbitrarily choose the reference 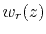 background to be the central trace of the reference
background to be the central trace of the reference
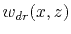 . Figure 9 shows the final estimated values of the three quantities--
. Figure 9 shows the final estimated values of the three quantities--
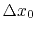 ,
,
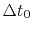 , and
, and 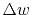 . Their corresponding errors are shown in Figure 10 suggesting a reasonable accuracy of the proposed method when the true velocity is close to the reference
. Their corresponding errors are shown in Figure 10 suggesting a reasonable accuracy of the proposed method when the true velocity is close to the reference  in the middle of the model. Higher errors are observed as the velocity difference becomes larger closer to the side and bottom edges.
in the middle of the model. Higher errors are observed as the velocity difference becomes larger closer to the side and bottom edges.
|
|---|
model-grad
Figure 7. The true velocity squared (top) of the linear gradient model (equation 23). Analytical  (middle) is overlaid by image rays. Analytical
(middle) is overlaid by image rays. Analytical  (bottom) is overlaid by contours showing propagating image wavefront.
(bottom) is overlaid by contours showing propagating image wavefront.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
input-grad
Figure 8. Inputs of the proposed time-to-depth conversion for the linear gradient model. The last input 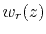 (not shown here) is taken to be the central trace of
(not shown here) is taken to be the central trace of
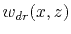 (top) in this case.
(top) in this case.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
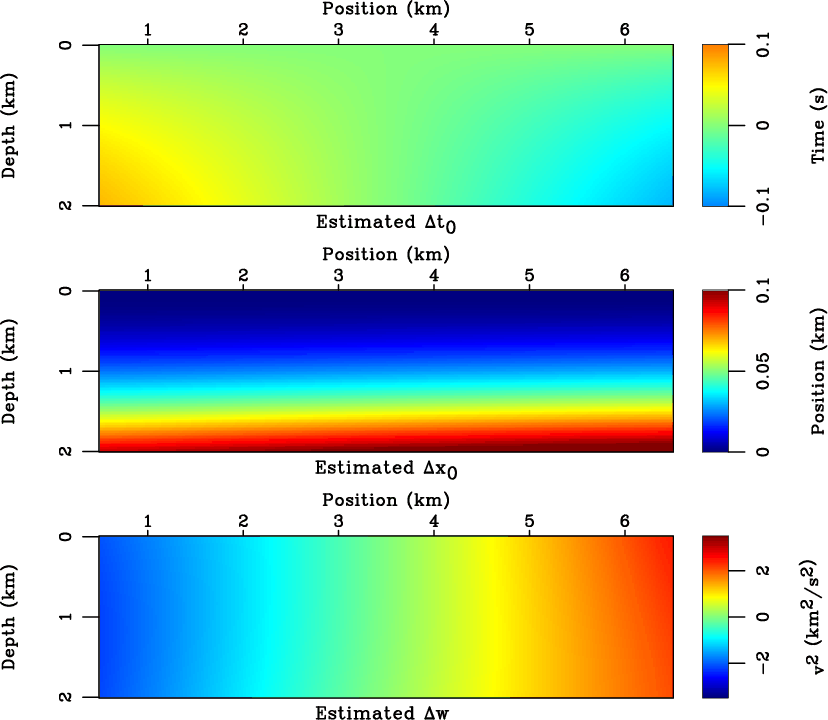
estcompare-grad
Figure 9. The estimated values of
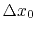 ,
,
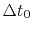 ,
, 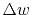 in the linear gradient model (equation 23).
in the linear gradient model (equation 23).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
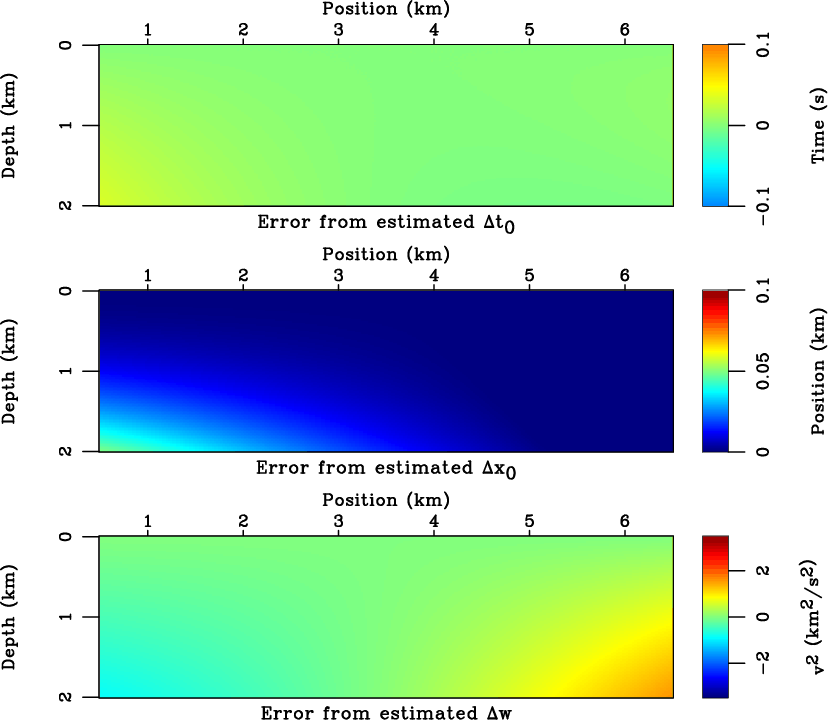
errcompare-grad
Figure 10. The errors of the estimated values of
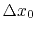 ,
,
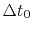 ,
, 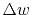 in comparison with the true values in the linear gradient model (equation 23). The errors are small for all estimated parameters except in the vicinity of the side and bottom edges of the model, which could be attributed to the growing difference between the true value of
in comparison with the true values in the linear gradient model (equation 23). The errors are small for all estimated parameters except in the vicinity of the side and bottom edges of the model, which could be attributed to the growing difference between the true value of 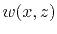 in that region and the reference
in that region and the reference 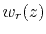 in the middle of the model.
in the middle of the model.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Fast time-to-depth conversion and interval velocity estimation in the case of weak lateral variations |  |
![[pdf]](icons/pdf.png) |
Next: Land field data example
Up: Examples
Previous: Linear sloth model
2018-11-16
![]() and
and ![]() overlaid by the contours that show image rays and propagating image wavefront. Figure 8 shows other inputs for the proposed conversion method. Again, we arbitrarily choose the reference
overlaid by the contours that show image rays and propagating image wavefront. Figure 8 shows other inputs for the proposed conversion method. Again, we arbitrarily choose the reference ![]() background to be the central trace of the reference
background to be the central trace of the reference
![]() . Figure 9 shows the final estimated values of the three quantities--
. Figure 9 shows the final estimated values of the three quantities--
![]() ,
,
![]() , and
, and ![]() . Their corresponding errors are shown in Figure 10 suggesting a reasonable accuracy of the proposed method when the true velocity is close to the reference
. Their corresponding errors are shown in Figure 10 suggesting a reasonable accuracy of the proposed method when the true velocity is close to the reference ![]() in the middle of the model. Higher errors are observed as the velocity difference becomes larger closer to the side and bottom edges.
in the middle of the model. Higher errors are observed as the velocity difference becomes larger closer to the side and bottom edges.



