 |
 |
 |
 | Fast time-to-depth conversion and interval velocity estimation in the case of weak lateral variations |  |
![[pdf]](icons/pdf.png) |
Next: Linear gradient model
Up: Examples
Previous: Examples
We first test the proposed method using a synthetic model with known analytical time-to-depth conversion solutions. In this model, the exact velocity squared is given by
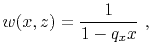 |
(22) |
where 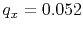 , which gives a maximum of 25
, which gives a maximum of 25 changes in lateral velocity along the 7
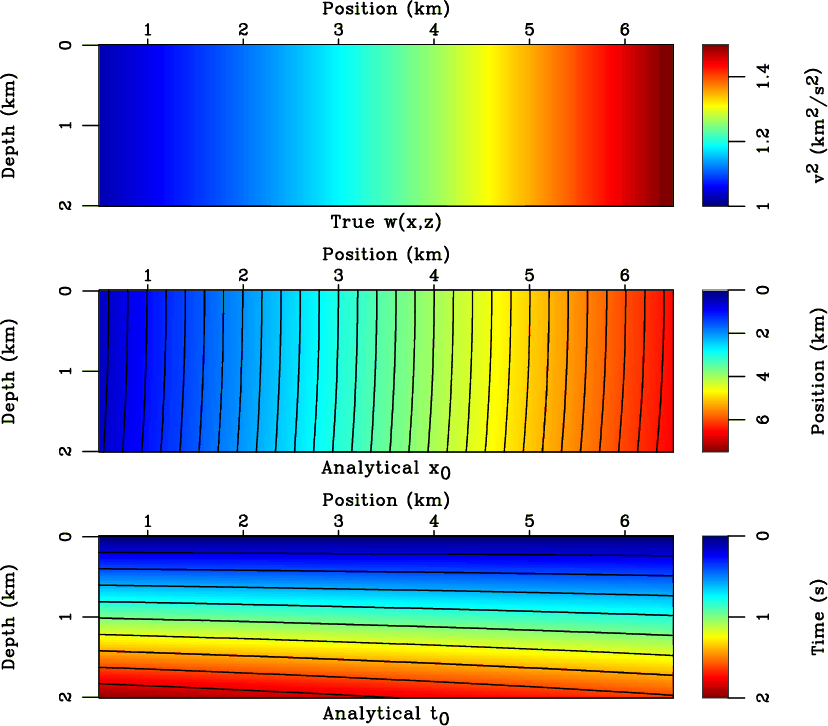
changes in lateral velocity along the 7  lateral extent of the model. The analytical solutions to time-to-depth conversion in this particular type of model were presented by Li and Fomel (2015). Figure 3 shows the true interval velocity of the model (equation 22), and the analytical
lateral extent of the model. The analytical solutions to time-to-depth conversion in this particular type of model were presented by Li and Fomel (2015). Figure 3 shows the true interval velocity of the model (equation 22), and the analytical 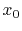 and
and 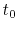 overlaid by the contours indicating image rays and propagating image wavefront. Other inputs for the proposed conversion method are shown in Figure 4. We choose the reference
overlaid by the contours indicating image rays and propagating image wavefront. Other inputs for the proposed conversion method are shown in Figure 4. We choose the reference 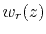 background to be the central trace of the reference
background to be the central trace of the reference
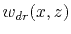 , which is constant in this case. The estimated results are shown in Figure 5 and their corresponding errors in comparison with the analytical values are shown in Figure 6. The errors appear to be generally small indicating a good accuracy for all estimated parameters but increase closer to the edges of the model, which are further away from the chosen reference
, which is constant in this case. The estimated results are shown in Figure 5 and their corresponding errors in comparison with the analytical values are shown in Figure 6. The errors appear to be generally small indicating a good accuracy for all estimated parameters but increase closer to the edges of the model, which are further away from the chosen reference 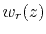 .
.
|
|---|
model-slow
Figure 3. The true velocity squared (top) of the linear sloth model (equation 22). Analytical 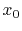 (middle) is overlaid by image rays. Analytical
(middle) is overlaid by image rays. Analytical 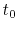 (bottom) is overlaid by contours showing propagating image wavefront.
(bottom) is overlaid by contours showing propagating image wavefront.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
input-slow
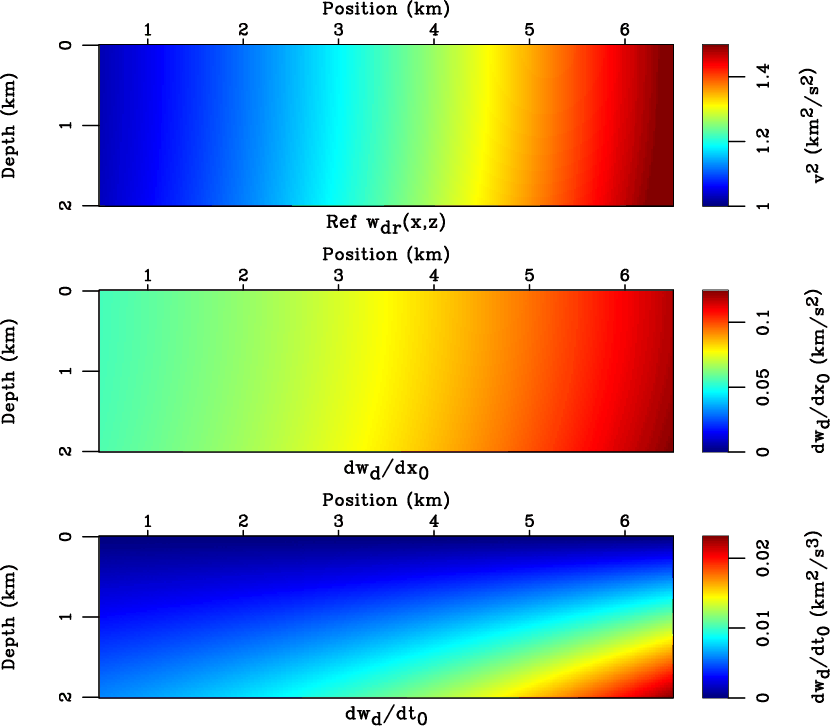
Figure 4. Inputs of the proposed time-to-depth conversion for the linear gradient model. The last input 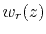 (not shown here) is taken to be the central trace of
(not shown here) is taken to be the central trace of
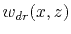 (top) in this case.
(top) in this case.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
estcompare-slow
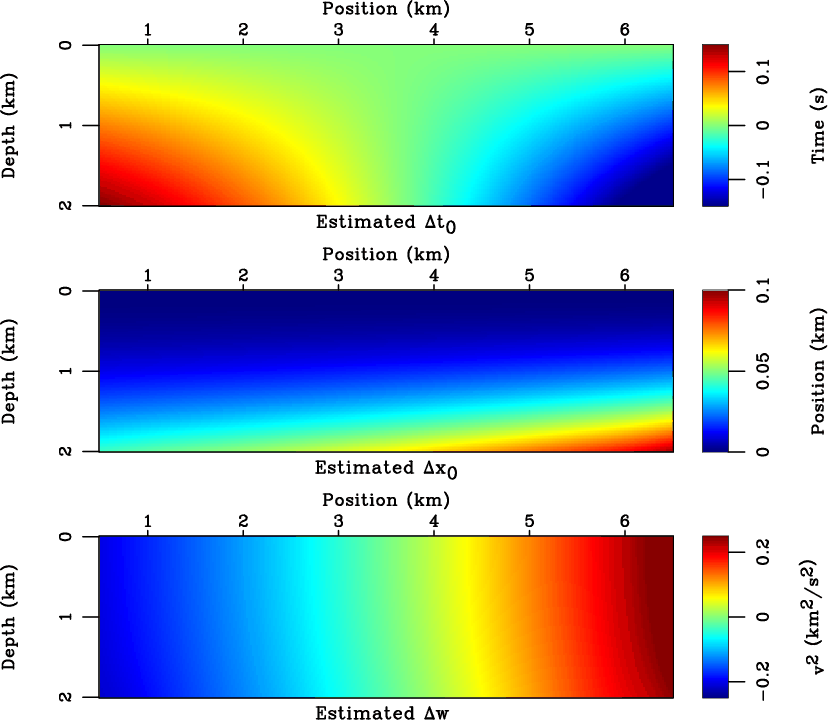
Figure 5. The estimated values of
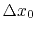 ,
,
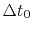 ,
, 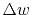 in the linear sloth model (equation 22).
in the linear sloth model (equation 22).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
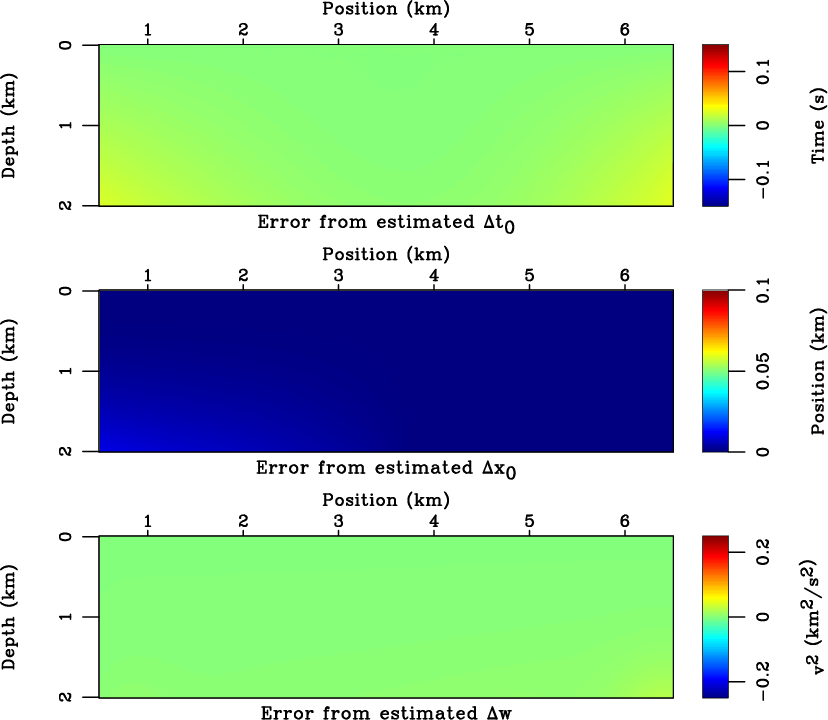
errcompare-slow
Figure 6. The errors of the estimated values of
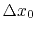 ,
,
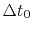 ,
, 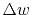 in comparison with the true values in the linear sloth model (equation 22). The errors are small for all estimated parameters indicating a good accuracy of the proposed method.
in comparison with the true values in the linear sloth model (equation 22). The errors are small for all estimated parameters indicating a good accuracy of the proposed method.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Fast time-to-depth conversion and interval velocity estimation in the case of weak lateral variations |  |
![[pdf]](icons/pdf.png) |
Next: Linear gradient model
Up: Examples
Previous: Examples
2018-11-16



