The structure-oriented SVD (SOSVD) refers to two processes: flattening along the local structure in a local spatial window and applying GSVD in the flattened local spatial window. The procedures can be summarized as:
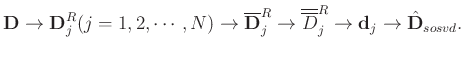 |
(6) |
Here,
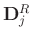 denotes the
denotes the 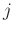 th spatial window (corresponding to
th spatial window (corresponding to 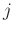 th trace) with a radius of
th trace) with a radius of 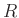 ,
,
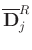 denotes the flattened local spatial window,
denotes the flattened local spatial window,
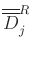 denotes the SVD denoised local spatial window,
denotes the SVD denoised local spatial window,
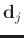 denotes the averaged local spatial window, and
denotes the averaged local spatial window, and
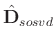 denotes the output data using SOSVD.
denotes the output data using SOSVD.
As we can see from the workflow, the key step that distinguishes SOSVD with other types of SVD approaches is the flattening in the local spatial window. The flattening corresponds to applying a flattening operator to the data (here we use a prediction operator according to local slope) so that the output data have horizontal events:
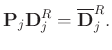 |
(7) |
where
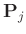 is the
is the 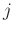 th flattening operator. Here, the flattening operator is chosen as a plane-wave prediction operator related with the local slope.
Equation 7 has the following detailed form:
th flattening operator. Here, the flattening operator is chosen as a plane-wave prediction operator related with the local slope.
Equation 7 has the following detailed form:
![\begin{displaymath}\begin{split}
& \left[
\begin{array}{cccccc}
\mathbf{P}_{(1,j...
...}_{1+R,j}, \cdots, \overline{\mathbf{d}}_{1+2R,j}].
\end{split}\end{displaymath}](img51.png) |
(8) |
Here,
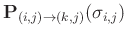 denotes the prediction operator from trace
denotes the prediction operator from trace 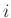 to trace
to trace 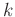 in
in 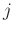 th spatial window, which is connected with the local slope of
th spatial window, which is connected with the local slope of 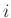 th trace. Prediction of a trace consists of shifting the original trace along dominant event slopes (Fomel, 2010).
Prediction of a trace from a distant neighbour can be accomplished by simple recursion (Liu et al., 2010), i.e., predicting trace
th trace. Prediction of a trace consists of shifting the original trace along dominant event slopes (Fomel, 2010).
Prediction of a trace from a distant neighbour can be accomplished by simple recursion (Liu et al., 2010), i.e., predicting trace 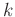 from trace
from trace 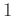 is simply
is simply
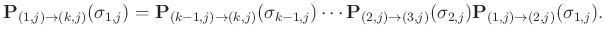 |
(9) |
The prediction operator is a numerical solution of the local plane differential equation
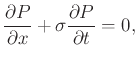 |
(10) |
for local plane wave propagation in the 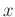 direction.
direction.
The dominant slopes are estimated by solving the following least-square minimization problem using regularized least-squares optimization:
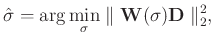 |
(11) |
where
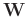 is the destruction operator defined as
is the destruction operator defined as
where
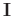 stands for the identity operator, and
stands for the identity operator, and
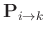 describes prediction of trace
describes prediction of trace 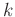 from trace
from trace 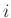 (same as the previous version
(same as the previous version
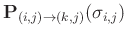 except for not in a specific spatial window). The optimization approach as shown in equation 11 for obtaining local slope estimation is called plane wave destruction (PWD) (Fomel, 2002).
except for not in a specific spatial window). The optimization approach as shown in equation 11 for obtaining local slope estimation is called plane wave destruction (PWD) (Fomel, 2002).
2020-03-09
![]() denotes the
denotes the ![]() th spatial window (corresponding to
th spatial window (corresponding to ![]() th trace) with a radius of
th trace) with a radius of ![]() ,
,
![]() denotes the flattened local spatial window,
denotes the flattened local spatial window,
![]() denotes the SVD denoised local spatial window,
denotes the SVD denoised local spatial window,
![]() denotes the averaged local spatial window, and
denotes the averaged local spatial window, and
![]() denotes the output data using SOSVD.
denotes the output data using SOSVD.
![\begin{displaymath}
\mathbf{W} = \left[
\begin{array}{ccccc}
\mathbf{I} & 0 & 0...
...hbf{P}}_{N-1\rightarrow N} & \mathbf{I}
\end{array}\right]\;,
\end{displaymath}](img60.png)