 |
 |
 |
 | Lowrank seismic wave extrapolation on a staggered grid |  |
![[pdf]](icons/pdf.png) |
Next: Lowrank FD for first-order
Up: Theory
Previous: Second-order and first-order mixed-domain
In this section, we apply lowrank decomposition to approximate the extrapolation operator in equation 9. As indicated by Fomel et al. (2013b,2010), the mixed-domain matrix in equation 9, taking
 as an example,
as an example,
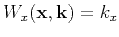 sinc sinc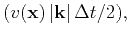 |
(11) |
can be efficiently decomposed into a separated representation as follows:
 |
(12) |
where
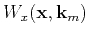 is a submatrix of
is a submatrix of
 which consists of selected columns associated with
which consists of selected columns associated with
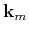 ;
;
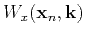 is another submatrix that contains selected rows associated with
is another submatrix that contains selected rows associated with
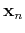 ; and
; and 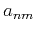 stands for middle matrix coefficients. The numerical construction of the separated representation in equation 12 follows the method of Engquist and Ying (2009).
stands for middle matrix coefficients. The numerical construction of the separated representation in equation 12 follows the method of Engquist and Ying (2009).
Using representation 12, we can calculate
 using a small number of fast Fourier transforms (FFTs), because
using a small number of fast Fourier transforms (FFTs), because
![$\displaystyle \displaystyle \frac{\partial p(\mathbf{x},t)}{\partial^+x} \appro...
...x/2}W_x(\mathbf{x}_n, \mathbf{k})\mathbf{F}\left[p(\mathbf{x},t)\right]\right].$](img79.png) |
(13) |
The same lowrank decomposition approach can be applied to the remaining three partial derivative operators in equation 9. Evaluation of equation 13 only needs 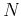 inverse FFTs, whose computational cost is
inverse FFTs, whose computational cost is
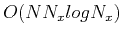 . However a straightforward application of equation 9 needs computational cost of
. However a straightforward application of equation 9 needs computational cost of 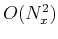 , where
, where 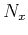 is the total size of the space grid.
is the total size of the space grid. 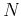 is related to the rank of the decomposed mixed-domain matrix 12, which is usually significantly smaller than
is related to the rank of the decomposed mixed-domain matrix 12, which is usually significantly smaller than 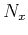 . Note that the number of FFTs
. Note that the number of FFTs 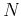 also depends on the given error level of lowrank decomposition with a predetermined
also depends on the given error level of lowrank decomposition with a predetermined  . Thus a complex model or increasing the time interval size
. Thus a complex model or increasing the time interval size  may increase the rank of the approximation matrix and correspondingly
may increase the rank of the approximation matrix and correspondingly 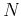 . In the numerical examples in this paper, the values of rank are usually between
. In the numerical examples in this paper, the values of rank are usually between 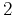 and
and 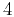 . Lowrank decomposition saves cost in calculating equations 9 and 10. We propose to apply it for seismic wave extrapolation in variable velocity and density media on a staggered grid. We call this method staggered grid lowrank(SGL) method.
. Lowrank decomposition saves cost in calculating equations 9 and 10. We propose to apply it for seismic wave extrapolation in variable velocity and density media on a staggered grid. We call this method staggered grid lowrank(SGL) method.
 |
 |
 |
 | Lowrank seismic wave extrapolation on a staggered grid |  |
![[pdf]](icons/pdf.png) |
Next: Lowrank FD for first-order
Up: Theory
Previous: Second-order and first-order mixed-domain
2014-06-02
 as an example,
as an example,
 using a small number of fast Fourier transforms (FFTs), because
using a small number of fast Fourier transforms (FFTs), because