Sparse weighting function

The output of equation 4 is immediately useful for determining passive source locations. However, the phase information is still unavailable and, additionally, the local normalization compromises amplitude. In order to obtain the original phase and amplitude information available in the time-reversal wavefield (equation 1), we propose to convert 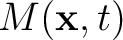$M(\mathbf{x},t)$ into a diagonal weighting function that projects the time-reversal wavefield into the space of admissible models. By selecting a thresholding value $\lambda \in [0,1]$, we calculate the weighting function using the Tukey (tapered cosine) window:

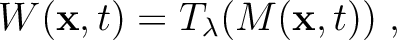$$W(\mathbf{x},t) = T_{\lambda}(M(\mathbf{x},t)) \;,$$ (5)

$$\begin{align*}T_{\lambda}(x) = \begin{cases} \frac{1}{2} \left[ 1+\cos\left(\pi ... ...ght) \right) \right], &x<\lambda \\ 1, &x > \lambda \end{cases} \;.\end{align*}$$ (6)

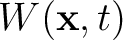$W(\mathbf{x},t)$ is essentially a projection operator that contains ones at all possible source locations and zeros otherwise. The Tukey window is intended for a smooth transition from zero to one, and can be replaced by other types of window functions. The time-reversal wavefield weighted by 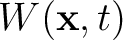$W(\mathbf{x},t)$ carries both the amplitude and phase information, but only at locations and times corresponding to possible sources.