 |
 |
 |
 | Theory of interval traveltime parameter estimation in layered anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Interval parameter estimation
Up: Sripanich & Fomel: Interval
Previous: Traveltime expansion
Using equations 9 and 10 and applying the chain rule, we can differentiate the one-way traveltime 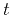 with respect to half offset
with respect to half offset 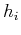 to derive the following equations:
to derive the following equations:
where the derivatives with respect to 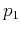 and
and 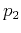 are represented by comma (e.g,
are represented by comma (e.g,
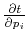 corresponds to
corresponds to 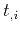 ),
),
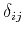 denotes the Kronecker delta,
denotes the Kronecker delta, 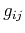 denotes
denotes
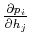 , and
, and 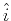 ,
, 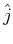 ,
, 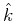 ,
, 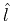 represent dummy indices. Equations 11-14 can be used to compute
represent dummy indices. Equations 11-14 can be used to compute 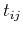 and
and 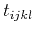 terms needed by equations 5 and 6 using explicit relationships for
terms needed by equations 5 and 6 using explicit relationships for
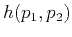 and
and
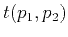 .
.
According to the chain rule and the symmetry of the time derivative tensors, the second-derivative tensor 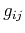 and its derivatives in equations 13 and 14 can be related to the derivatives of half offset
and its derivatives in equations 13 and 14 can be related to the derivatives of half offset 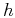 as follows:
as follows:
where 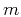 ,
, 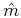 ,
, 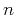 ,
, 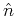 are dummy indices. The matrix
are dummy indices. The matrix
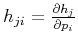 is the inverse of the matrix
is the inverse of the matrix 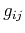 (Grechka and Tsvankin, 1998). Substituting equations 15 and 16 into equations 13 and 14, we subsequently arrive at expressions
(Grechka and Tsvankin, 1998). Substituting equations 15 and 16 into equations 13 and 14, we subsequently arrive at expressions
which only involve derivatives of explicitly defined functions. Subsequently, we have at zero offset (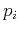 =0):
=0):
Subsections
 |
 |
 |
 | Theory of interval traveltime parameter estimation in layered anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Interval parameter estimation
Up: Sripanich & Fomel: Interval
Previous: Traveltime expansion
2017-04-14
![]() with respect to half offset
with respect to half offset ![]() to derive the following equations:
to derive the following equations:
![]() and its derivatives in equations 13 and 14 can be related to the derivatives of half offset
and its derivatives in equations 13 and 14 can be related to the derivatives of half offset ![]() as follows:
as follows: