We begin our review based on 1D vectors
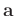 and
and
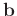 . A common way to measure the similarity between two signals is to calculate the correlation coefficient,
. A common way to measure the similarity between two signals is to calculate the correlation coefficient,
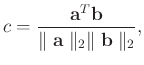 |
(40) |
where 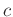 is the correlation coefficient,
is the correlation coefficient,
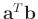 denotes the dot product of
denotes the dot product of
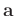 and
and
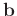 .
.
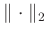 denotes the
denotes the 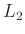 norm of the input vector. The correlation coefficient
norm of the input vector. The correlation coefficient 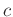 can measure the correlation, or in other words similarity, between two vectors within the selected window in a global manner. However, in some specific applications, a local measurement for the similarity is more demanded. In order to
measure the local similarity of two vectors, it is straightforwardly to apply local windows to the target vectors:
can measure the correlation, or in other words similarity, between two vectors within the selected window in a global manner. However, in some specific applications, a local measurement for the similarity is more demanded. In order to
measure the local similarity of two vectors, it is straightforwardly to apply local windows to the target vectors:
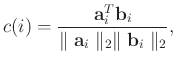 |
(41) |
where
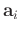 and
and
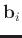 denote the localized vectors centered on the
denote the localized vectors centered on the 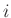 th entry of input long vectors
th entry of input long vectors
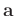 and
and
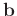 , respectively. The windowing is sometime troublesome, since the measured similarity is largely dependent on the windowing length and the measured local similarity might be discontinuous because of the separate calculations in windows. To avoid the negative performance caused by local windowing calculations, Fomel (2007) proposed an elegant way for calculating smooth local similarity via solving two inverse problems.
, respectively. The windowing is sometime troublesome, since the measured similarity is largely dependent on the windowing length and the measured local similarity might be discontinuous because of the separate calculations in windows. To avoid the negative performance caused by local windowing calculations, Fomel (2007) proposed an elegant way for calculating smooth local similarity via solving two inverse problems.
Let us first rewrite equation C-1 in a different form. Getting the absolute value of both sides of equation C-1, considering
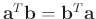 , we have
, we have
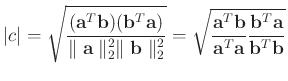 |
(42) |
We let
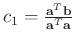 and
and
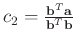 , equation C-3 turns to
, equation C-3 turns to
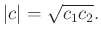 |
(43) |
It is obvious that scalars 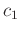 and
and 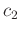 come from two least-squares inverse problem:
come from two least-squares inverse problem:
The local similarity attribute is based on equations C-5 and C-6, but is in a localized version:
where
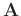 is a diagonal operator composed from the elements of
is a diagonal operator composed from the elements of
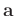 :
:
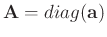 and
and
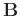 is a diagonal operator composed from the elements of
is a diagonal operator composed from the elements of
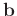 :
:
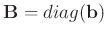 .
Equations C-7 and C-8 are solved via shaping regularization
.
Equations C-7 and C-8 are solved via shaping regularization
where
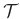 is a smoothing operator, and
is a smoothing operator, and 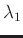 and
and 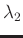 are two parameters controlling the physical dimensionality and enabling fast convergence when inversion is implemented iteratively. These two parameters can be chosen as
are two parameters controlling the physical dimensionality and enabling fast convergence when inversion is implemented iteratively. These two parameters can be chosen as
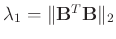 and
and
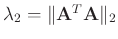 (Fomel, 2007).
(Fomel, 2007).
After the
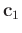 and
and
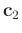 are solved, the localized version of
are solved, the localized version of 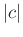 is
is
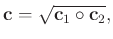 |
(50) |
where
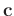 is the output local similarity and
is the output local similarity and 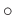 denotes element-wise product.
denotes element-wise product.
To calculate the 2D and 3D versions of local similarity, as used in demonstrating the reconstruction performance in the main contents of the paper, one needs to first reshape a 2D matrix or a 3D tensor into a 1D vector and then to use the formula shown above to calculate the local similarity vector. Since the local similarity is of the same size of the input two vectors, it can be easily reshaped into the 2D or 3D form for display purposes.
2020-12-05
![]() , we have
, we have
![]() and
and
![]() are solved, the localized version of
are solved, the localized version of ![]() is
is