 |
 |
 |
 | Elastic wave-vector decomposition in heterogeneous anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Elastic wave-vector decomposition
Up: Review of wave-mode separation
Previous: Review of wave-mode separation
According to the Helmholtz decomposition theory (Aki and Richards, 2002), a vector wavefield
 in homogeneous isotropic media can
be decomposed into P-wavefield (curl-free) and S-wavefield (divergence-free) components:
in homogeneous isotropic media can
be decomposed into P-wavefield (curl-free) and S-wavefield (divergence-free) components:
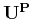 . The wavefield
. The wavefield
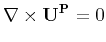 satisfies
satisfies
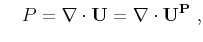 and and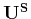 |
(1) |
while
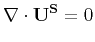 satisfies
satisfies
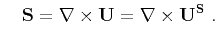 and and |
(2) |
In the Fourier domain, the equivalent expressions are
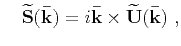 and and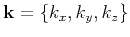 |
(3) |
where
 denotes the wave-vector, and
denotes the wave-vector, and
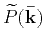 is its normalized quantity, which is similar to the unit phase direction.
is its normalized quantity, which is similar to the unit phase direction.
 and
and
 represent the scalar
represent the scalar 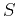 -wavefield and the vector
-wavefield and the vector 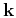 -wavefield in the Fourier domain respectively. In homogeneous anisotropic media, the P- and S- waves are not polarized parallel and perpendicular to the wave-vector direction (
-wavefield in the Fourier domain respectively. In homogeneous anisotropic media, the P- and S- waves are not polarized parallel and perpendicular to the wave-vector direction (
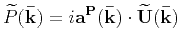 ) and therefore, expressions in equation 3 cannot separate the wavefield correctly. Dellinger and Etgen (1990) modified these operators for separating P and S waves in homogeneous TI media as follows:
) and therefore, expressions in equation 3 cannot separate the wavefield correctly. Dellinger and Etgen (1990) modified these operators for separating P and S waves in homogeneous TI media as follows:
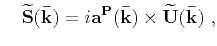 and and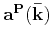 |
(4) |
where
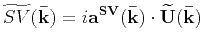 denotes the normalized polarization vector of P wave obtained by solving the Christoffel equation. Note that
denotes the normalized polarization vector of P wave obtained by solving the Christoffel equation. Note that
 contains the wavefield corresponding to both S-wave modes.
contains the wavefield corresponding to both S-wave modes.
Despite the validity of both operators in equation 4, the first expression has found more uses in practice because of its simplicity (Yan and Sava, 2009). In homogeneous TI media, one can separate scalar SV- and SH-wavefields using the following expressions:
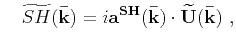 and and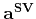 |
(5) |
with appropriately defined normalized polarization vectors of
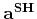 and
and
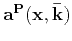 from the Christoffel equation.
For heterogeneous VTI media, the polarizations become dependent on the spatial locations and can be denoted as
from the Christoffel equation.
For heterogeneous VTI media, the polarizations become dependent on the spatial locations and can be denoted as
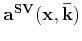 ,
,
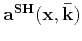 , and
, and
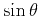 for proper usage in equations 4 and 5.
for proper usage in equations 4 and 5.
For efficient implementation in the space domain, Yan and Sava (2009) proposed to approximate these operators in heterogeneous VTI media as non-stationary filters. An application of this process is commonly referred to as wave-mode separation. Its extension to heterogeneous TTI media was proposed by Yan and Sava (2012). However,
the computational cost for this approach is large as it is proportional to the number of grids in the model and the size of each filter (Yan and Sava, 2011). To cope with S-wave singularities, Yan and Sava (2012) proposed to scale the displacements corresponding to the two S-wave modes by
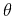 , where
, where 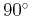 is the polar angle from the symmetry axis. This method produces uniformly scaled elastic wavefields of the two S-wave modes with zero amplitude along the symmetry axis where the kiss singularities are located. As a downside, the final separated scalar wavefields suffer from both
is the polar angle from the symmetry axis. This method produces uniformly scaled elastic wavefields of the two S-wave modes with zero amplitude along the symmetry axis where the kiss singularities are located. As a downside, the final separated scalar wavefields suffer from both  phase shift from the
phase shift from the 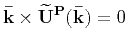 factor and incorrect amplitudes from
factor and incorrect amplitudes from
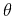 scaling and may not be applicable to true-amplitude imaging techniques.
scaling and may not be applicable to true-amplitude imaging techniques.
 |
 |
 |
 | Elastic wave-vector decomposition in heterogeneous anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Elastic wave-vector decomposition
Up: Review of wave-mode separation
Previous: Review of wave-mode separation
2017-04-18
![]() , where
, where ![]() is the polar angle from the symmetry axis. This method produces uniformly scaled elastic wavefields of the two S-wave modes with zero amplitude along the symmetry axis where the kiss singularities are located. As a downside, the final separated scalar wavefields suffer from both
is the polar angle from the symmetry axis. This method produces uniformly scaled elastic wavefields of the two S-wave modes with zero amplitude along the symmetry axis where the kiss singularities are located. As a downside, the final separated scalar wavefields suffer from both ![]() phase shift from the
phase shift from the ![]() factor and incorrect amplitudes from
factor and incorrect amplitudes from
![]() scaling and may not be applicable to true-amplitude imaging techniques.
scaling and may not be applicable to true-amplitude imaging techniques.