|
|
|
|
Elastic wave-vector decomposition in heterogeneous anisotropic media |
|
TRIc-11
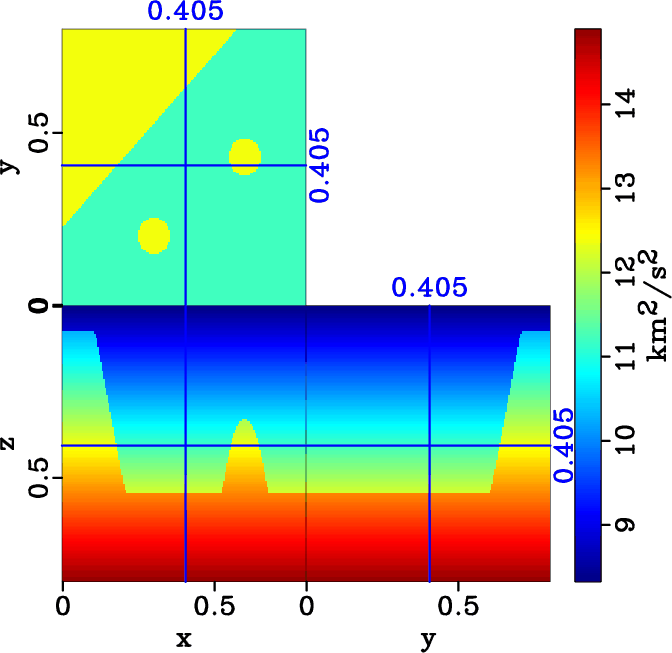
Figure 14. Density normalized |
|
|---|---|
|
|

|
|---|
|
TRIw-lr-x,TRIw-lr-y,TRIw-lr-z
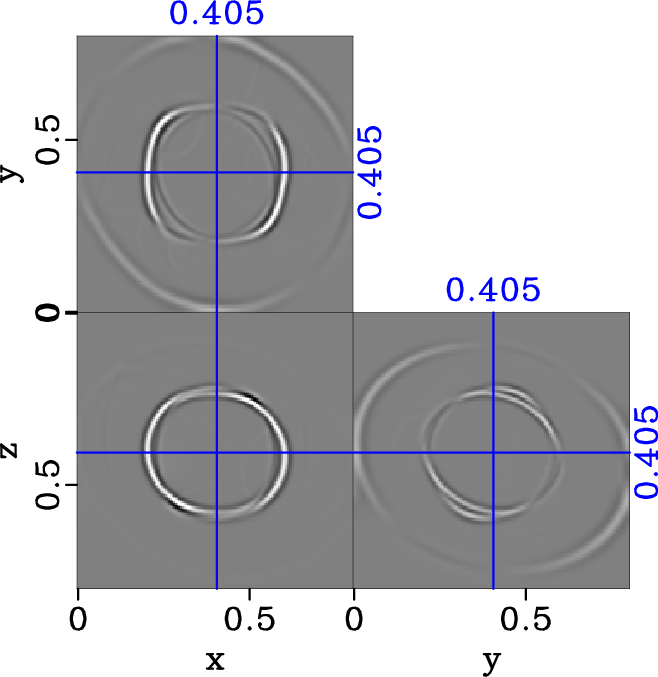
Figure 15. Original elastic wavefield in |
|
|
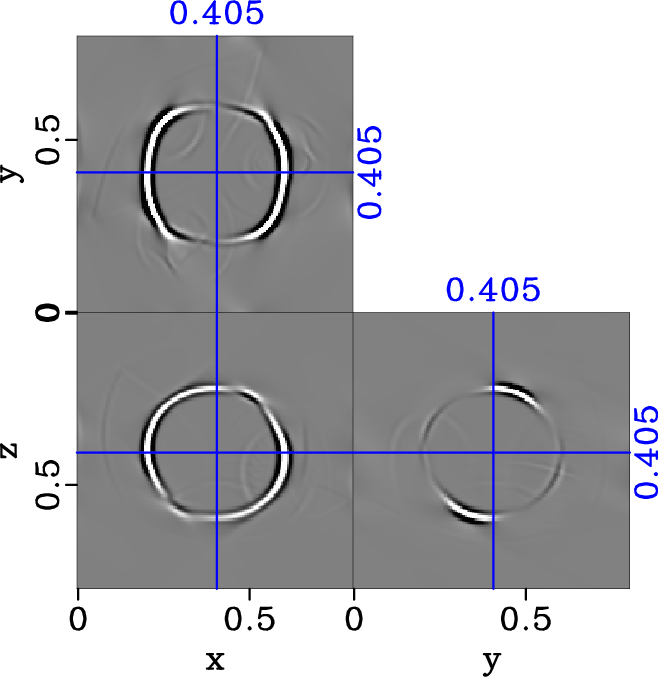

|
|---|
|
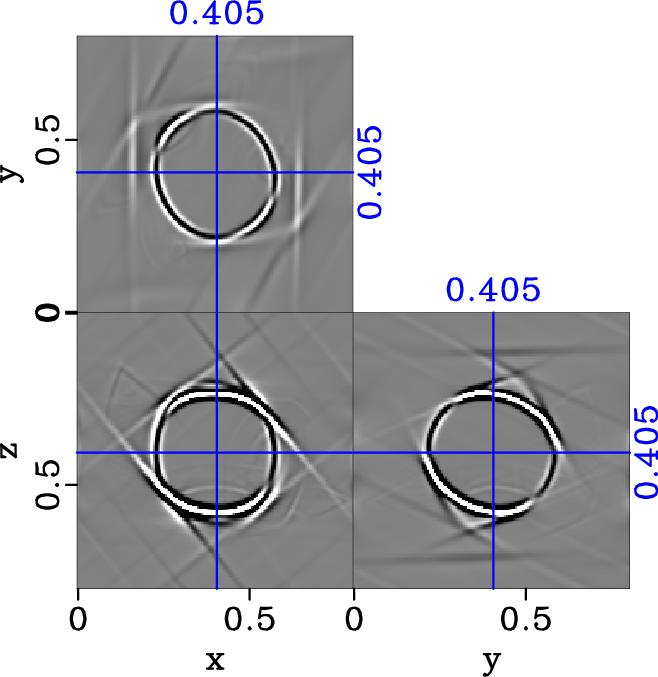
noTRIw-dlr-S1-y,TRIw-dlr-S1-y,comTRIw-dlr-S1-y
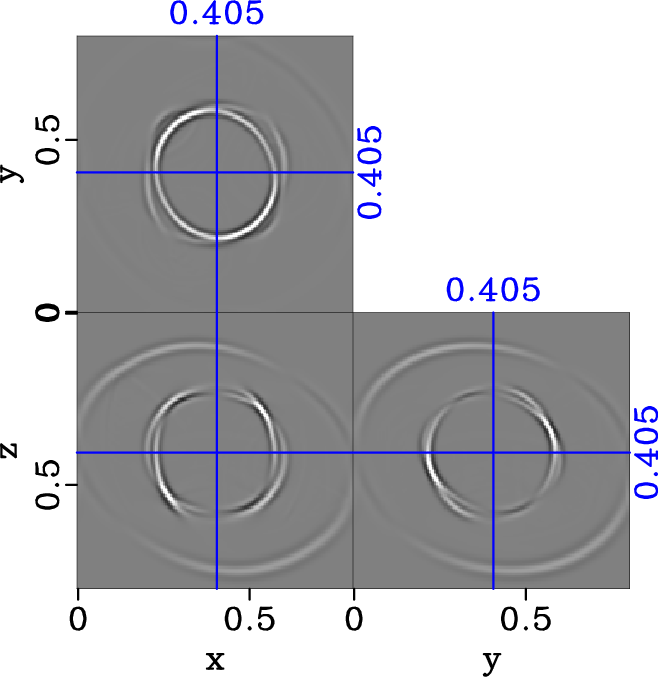
Figure 16. Separated y-component of S1 elastic wavefield in the two-layered heterogenous triclinic model (equation 29) with |
|
|
|
|---|
|
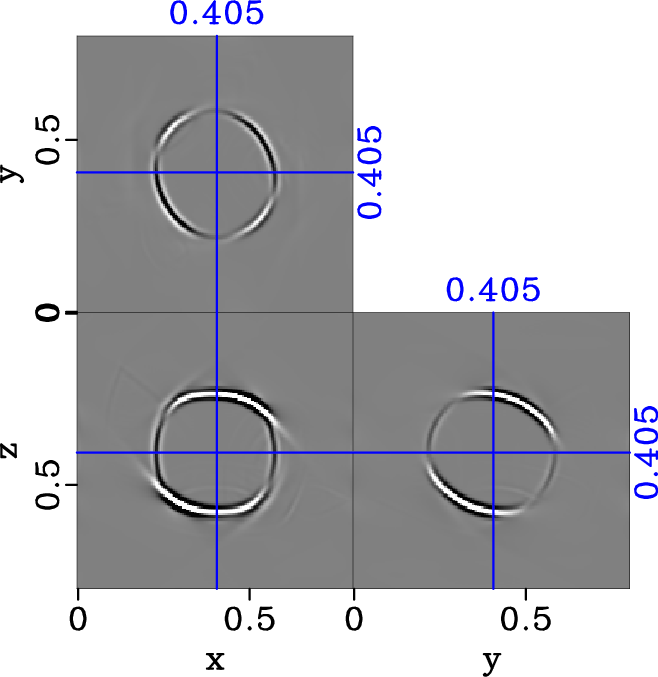
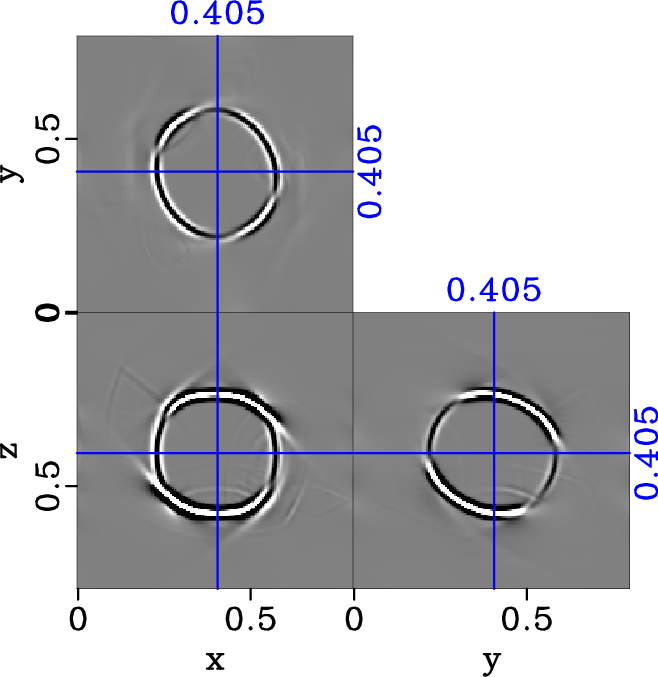
noTRIw-dlr-S2-y,TRIw-dlr-S2-y,comTRIw-dlr-S2-y
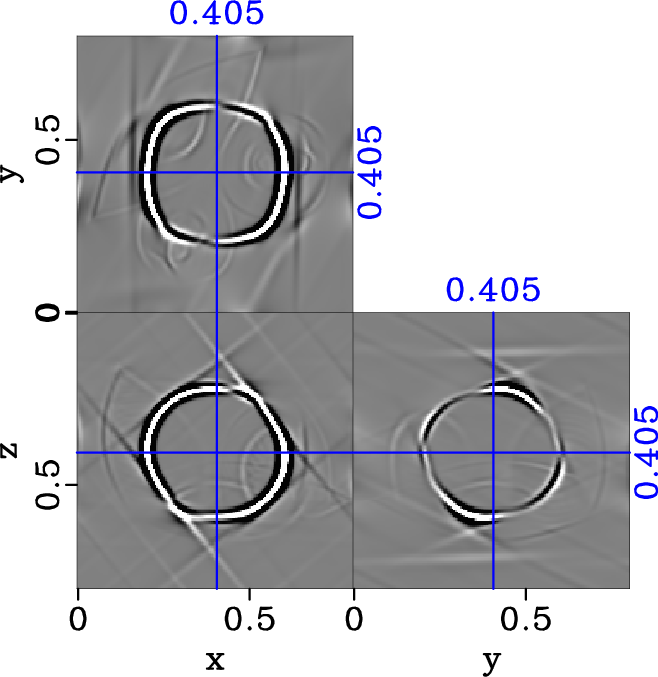
Figure 17. Separated y-component of S2 elastic wavefield in the two-layered heterogenous triclinic model (equation 29) with |
|
|
|
|
|
|
Elastic wave-vector decomposition in heterogeneous anisotropic media |