 |
 |
 |
 | Traveltime approximations for transversely isotropic media with an inhomogeneous background |  |
![[pdf]](icons/pdf.png) |
Next: Appendix B: Expansion in
Up: Alkhalifah: TI traveltimes in
Previous: Bibliography
To derive a traveltime equation in terms of perturbations in  , we first establish the form for the
governing equation for TI media given by the eikonal representation.
The eikonal equation for
, we first establish the form for the
governing equation for TI media given by the eikonal representation.
The eikonal equation for  -waves in TI media in 2D (for simplicity) is
given by
-waves in TI media in 2D (for simplicity) is
given by
| |
|
 |
|
| |
|
 |
(25) |
To
solve equation A-1 through perturbation theory, we assume that  is small, and thus, a trial solution can be expressed
as a series expansion in
is small, and thus, a trial solution can be expressed
as a series expansion in  given by
given by
 |
(26) |
where  ,
,  and
and  are coefficients of the expansion given in units of traveltime, and, for practicality,
terminated at the
second power of
are coefficients of the expansion given in units of traveltime, and, for practicality,
terminated at the
second power of  .
Inserting the trial solution, equation A-2, into equation A-1 yields a long formula, but by setting
.
Inserting the trial solution, equation A-2, into equation A-1 yields a long formula, but by setting  ,
I obtain the zeroth-order term given by
,
I obtain the zeroth-order term given by
 |
|
|
(27) |
which is the eikonal formula for VTI anisotropy. By equating the coefficients of the powers of the
independent parameter  , in succession,
we end up first with the coefficients of first-power in
, in succession,
we end up first with the coefficients of first-power in
 , simplified by using equation A-3, and given by
, simplified by using equation A-3, and given by
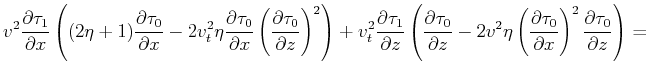 |
|
|
|
 |
|
|
(28) |
which is a first-order linear partial differential equation in  .
The coefficient of
.
The coefficient of
 , with some manipulation, has the
following form
, with some manipulation, has the
following form
which is again a first-order linear partial differential equation in
 with an obviously
more complicated source function given by the right-hand side.
Though the equation seems complicated, many of the variables of the source function (right-hand side) can be evaluated during the evaluation of
equations A-3 and A-4 in a fashion that will not add much to the cost.
with an obviously
more complicated source function given by the right-hand side.
Though the equation seems complicated, many of the variables of the source function (right-hand side) can be evaluated during the evaluation of
equations A-3 and A-4 in a fashion that will not add much to the cost.
 |
 |
 |
 | Traveltime approximations for transversely isotropic media with an inhomogeneous background |  |
![[pdf]](icons/pdf.png) |
Next: Appendix B: Expansion in
Up: Alkhalifah: TI traveltimes in
Previous: Bibliography
2013-04-02
![]() , we first establish the form for the
governing equation for TI media given by the eikonal representation.
The eikonal equation for
, we first establish the form for the
governing equation for TI media given by the eikonal representation.
The eikonal equation for ![]() -waves in TI media in 2D (for simplicity) is
given by
-waves in TI media in 2D (for simplicity) is
given by