 |
 |
 |
 | Automatic traveltime picking using the instantaneous traveltime |  |
![[pdf]](icons/pdf.png) |
Next: The mapping operator
Up: Methodology
Previous: The mean and instantaneous
In principle any time-frequency representation can be used for the calculation of the instantaneous traveltime. An obvious choice is the short-time Fourier transform. However the short-time Fourier transform suffers from the time-frequency resolution limitation and therefore the length of the window used for its calculation significantly depends on the frequency content of the windowed data. It is therefore not appropriate for our problem.
Another alternative is provided by Liu et al. (2011). Their method essentially computes a series representation of a nonstationary, temporally bounded signal using the same basis functions as the Fourier series.
This series representation is therefore similar to the Fourier series, however, the series coefficients are allowed to be time-varying.
In particular, if
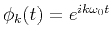 denote the basis functions of the Fourier series expansion for a signal
denote the basis functions of the Fourier series expansion for a signal 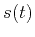 with support
with support
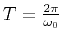 , then
, then 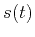 is represented as
is represented as
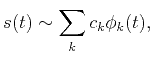 |
(5) |
where
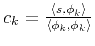 and
and
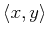 denotes the usual dot product of the
denotes the usual dot product of the
 space of functions with period
space of functions with period 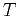 .
.
We note that equation 5 is equivalent to the
 -minimization problem:
-minimization problem:
 |
(6) |
Instead of using equation 6 to calculate constant Fourier series coefficients, Liu et al. (2011) calculate time-varying coefficients, 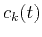 , which are the solution of the
, which are the solution of the
 -minimization problem:
-minimization problem:
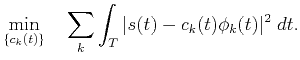 |
(7) |
Apart from the time-varying character of the coefficients, 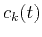 , in equation 7, equations 6 and 7 are also different in another significant way: in equation 6, the minimization is performed between the signal and its series representation, while in equation 7, the minimization is performed between the signal and every frequency component separately.
, in equation 7, equations 6 and 7 are also different in another significant way: in equation 6, the minimization is performed between the signal and its series representation, while in equation 7, the minimization is performed between the signal and every frequency component separately.
The coefficients, 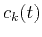 , can be computed by solving the regularized least-squares problem:
, can be computed by solving the regularized least-squares problem:
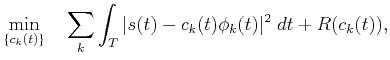 |
(8) |
where 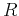 is the regularization operator (Liu et al., 2011).
Using such an approach enforces smoothness on the coefficients,
is the regularization operator (Liu et al., 2011).
Using such an approach enforces smoothness on the coefficients, 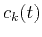 , which ensures the solution of the underdetermined problem 7 (Fomel, 2007b).
, which ensures the solution of the underdetermined problem 7 (Fomel, 2007b).
 |
 |
 |
 | Automatic traveltime picking using the instantaneous traveltime |  |
![[pdf]](icons/pdf.png) |
Next: The mapping operator
Up: Methodology
Previous: The mean and instantaneous
2013-04-02
![]() denote the basis functions of the Fourier series expansion for a signal
denote the basis functions of the Fourier series expansion for a signal ![]() with support
with support
![]() , then
, then ![]() is represented as
is represented as
![]() -minimization problem:
-minimization problem:
![]() , can be computed by solving the regularized least-squares problem:
, can be computed by solving the regularized least-squares problem: