|
|
|
|
Automatic traveltime picking using the instantaneous traveltime |
If ![]() is a band-limited delta function, then
is a band-limited delta function, then
![]() does not equal
does not equal ![]() but rather is approximately equal to
but rather is approximately equal to ![]() , within the bandwidth of
, within the bandwidth of ![]() (see Figure 1(a)). Consequently, the dependence of
(see Figure 1(a)). Consequently, the dependence of
![]() on frequency can be dropped by simply averaging
on frequency can be dropped by simply averaging
![]() within the bandwidth of
within the bandwidth of ![]() . In the case that
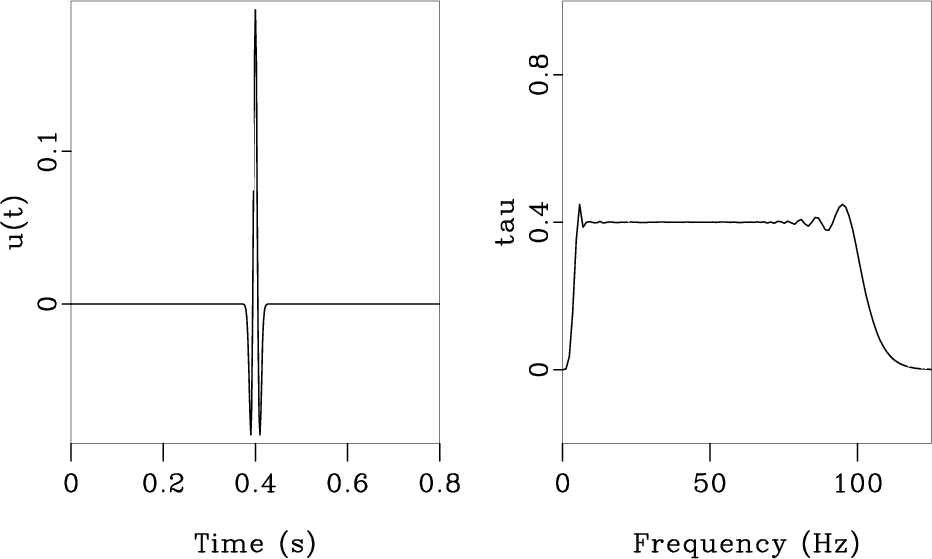
. In the case that ![]() is indeed a signal that signifies an event, such as the band-limited spike of Figure 1(a), averaging over the frequencies within the bandwidth of the signal yields a meaningful number, namely the time of occurrence of the event. On the other hand, if
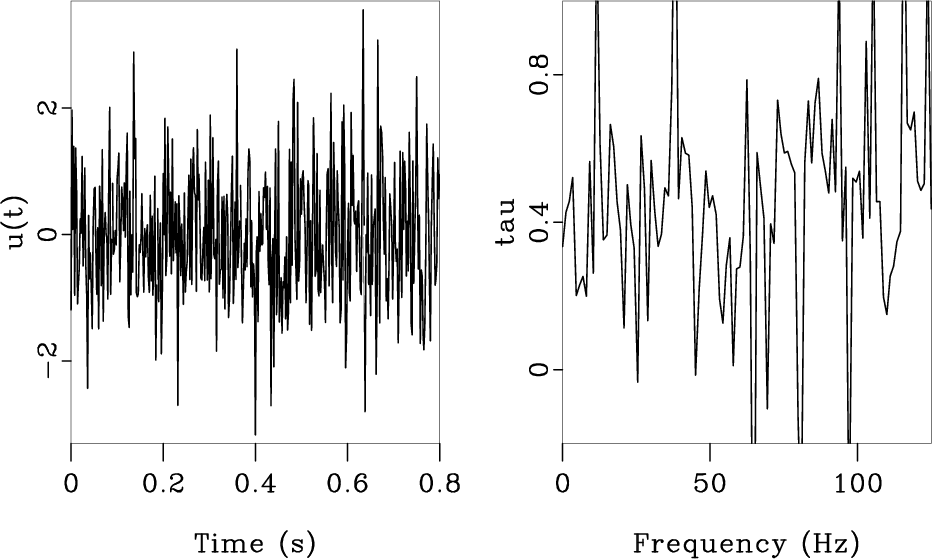
is indeed a signal that signifies an event, such as the band-limited spike of Figure 1(a), averaging over the frequencies within the bandwidth of the signal yields a meaningful number, namely the time of occurrence of the event. On the other hand, if ![]() is random noise or even insufficiently spiky, then
is random noise or even insufficiently spiky, then
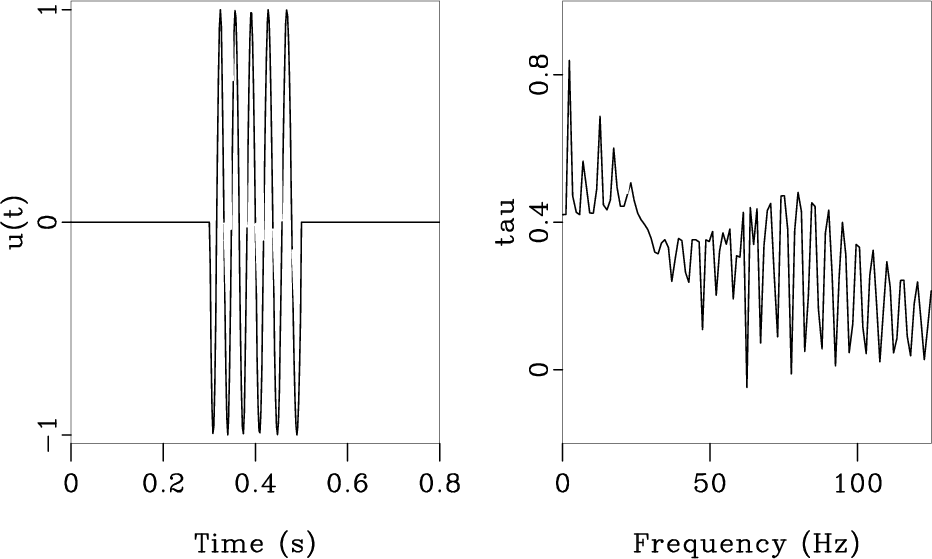
![]() varies considerably with frequency (Figures 1(b), 1(c)). In this case, averaging of
varies considerably with frequency (Figures 1(b), 1(c)). In this case, averaging of
![]() yields a meaningless number. This feature can be used to identify events in the seismic data.
yields a meaningless number. This feature can be used to identify events in the seismic data.
|
|---|
|
rick,noiz,chrp
Figure 1. Various signals (left) and their mean traveltimes as a function of frequency (right). (a) Band-limited spike. (b) Random noise. (c) Quasi-sinusoid (simulates Vibroseis harmonics). |
|
|
The quantity
![]() is essentially the derivative of the phase of
is essentially the derivative of the phase of ![]() with respect to frequency, also referred to as group delay or envelope delay. In fact it has been used as such by Stoffa et al. (1974) to compute a continuous phase curve and circumvent the phase-wrapping problem in homomorphic deconvolution. However, we prefer to use the term traveltime for reasons that are explained below.
with respect to frequency, also referred to as group delay or envelope delay. In fact it has been used as such by Stoffa et al. (1974) to compute a continuous phase curve and circumvent the phase-wrapping problem in homomorphic deconvolution. However, we prefer to use the term traveltime for reasons that are explained below.
If we assume a signal consisting of two spikes at ![]() and
and ![]() , respectively, i.e.,
, respectively, i.e.,
![]() , we get
, we get
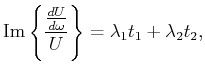 |
(2) |
From the above discussion, it is clear that the mean traveltime attribute is not much of use, if it is to be computed on the whole trace. The Fourier transform used in equation 1 performs an integration over the observed time interval. The localized temporal information is therefore lost. What is needed is a time-frequency transform to replace the Fourier transform in equation 1 such that the traveltime attribute becomes localized in time as well. In this way, different arrivals are isolated from one another and the computed traveltimes are more accurate. The instantaneous traveltime ![]() is therefore defined as
is therefore defined as
In the next two subsections, we discuss these two issues, namely the choices of the time-frequency transform and the mapping operator.
|
|
|
|
Automatic traveltime picking using the instantaneous traveltime |