|
|
|
|
Time migration velocity analysis by velocity continuation |
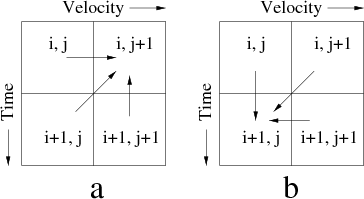
In the two-dimensional case, equation 5 reduces to a tridiagonal system of linear equations, which can be easily inverted. In 3-D, a straightforward extension can be obtained by using either directional splitting or helical schemes (Rickett et al., 1998). The direction of stable propagation is either forward in velocity and backward in time or backward in velocity and forward in time as shown in Figure 1.
|
vlcfds
Figure 1. Finite-difference scheme for the velocity continuation equation. A stable propagation is either forward in velocity and backward in time (a) or backward in velocity and forward in time (b). |
|
|---|---|
|
|
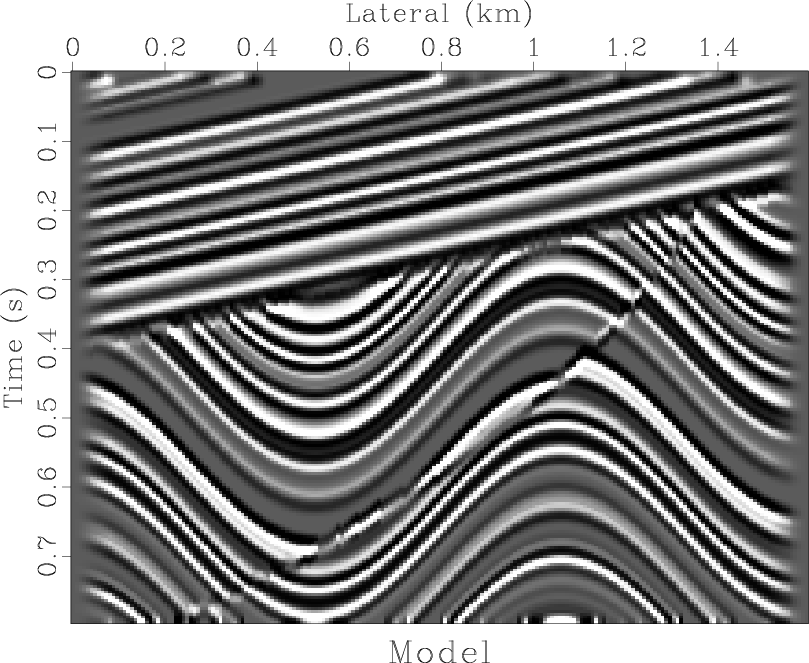
In order to test the performance of the finite-difference velocity
continuation method, I use a simple synthetic model from
Claerbout (1995). The reflectivity model is shown in
Figure 2. It contains several features that challenge the
migration performance: dipping beds, unconformity, syncline,
anticline, and fault. The velocity is taken to be constant
![]() .
.
|
mod
Figure 2. Synthetic model for testing finite-difference migration by velocity continuation. |
|
|---|---|
|
|
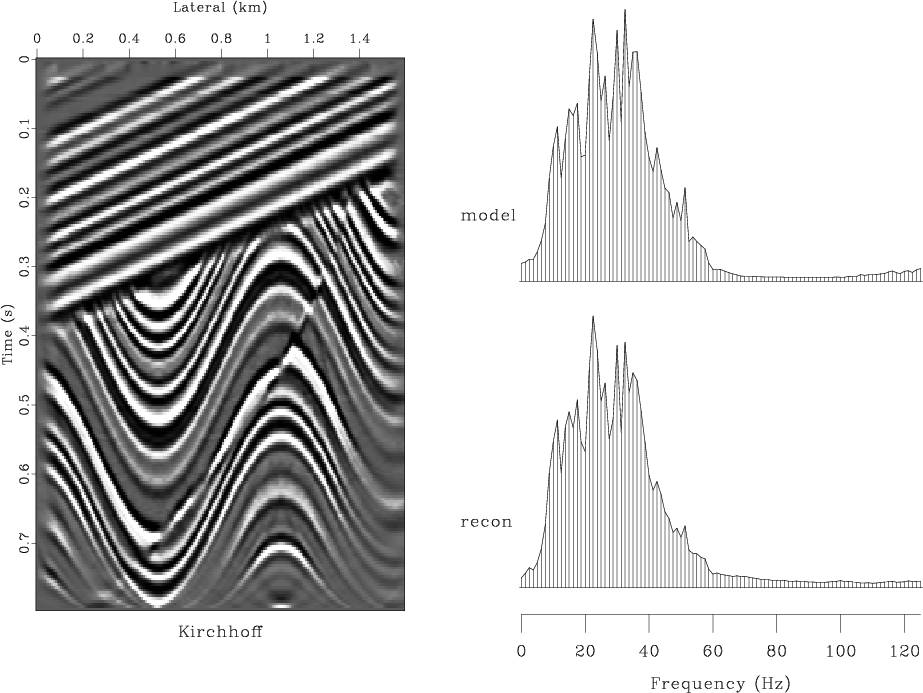
Figures 3-6(b) compare invertability of different
migration methods. In all cases, constant-velocity modeling (demigration)
was followed by migration with the correct velocity. Figures
3 and 4 show the results of modeling and
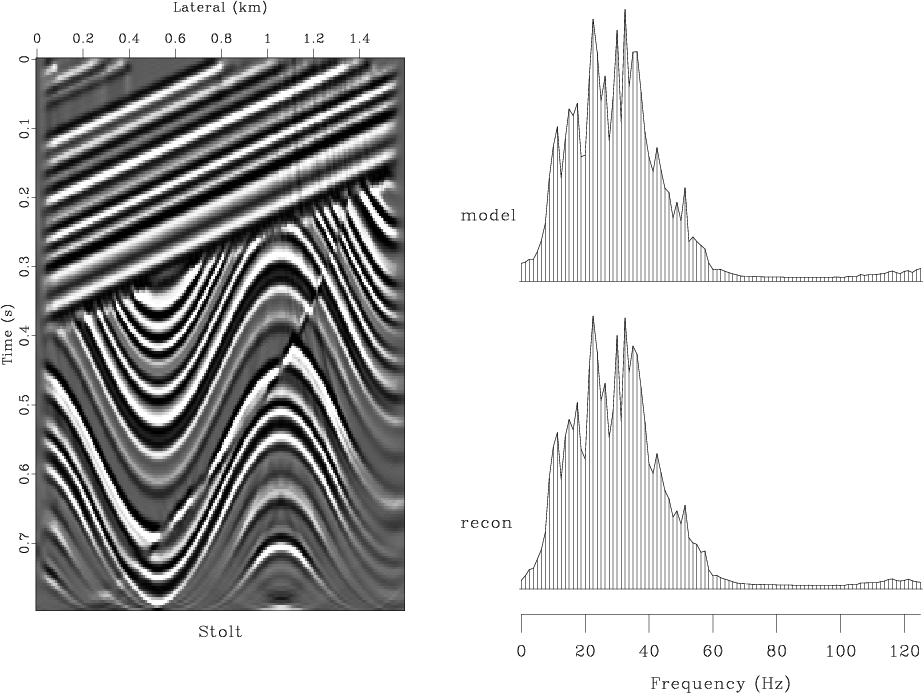
migration with the Kirchhoff (Schneider, 1978) and ![]() -
-![]() (Stolt, 1978) methods, respectively. These figures should
be compared with Figure 5, showing the analogous result
of the finite-difference velocity continuation. The comparison
reveals a remarkable invertability of velocity continuation, which
reconstructs accurately the main features and frequency content of the
model. Since the forward operators were different for different
migrations, this comparison did not test the migration properties
themselves. For such a test, I compare the results of the Kirchhoff
and velocity-continuation migrations after Stolt modeling. The result
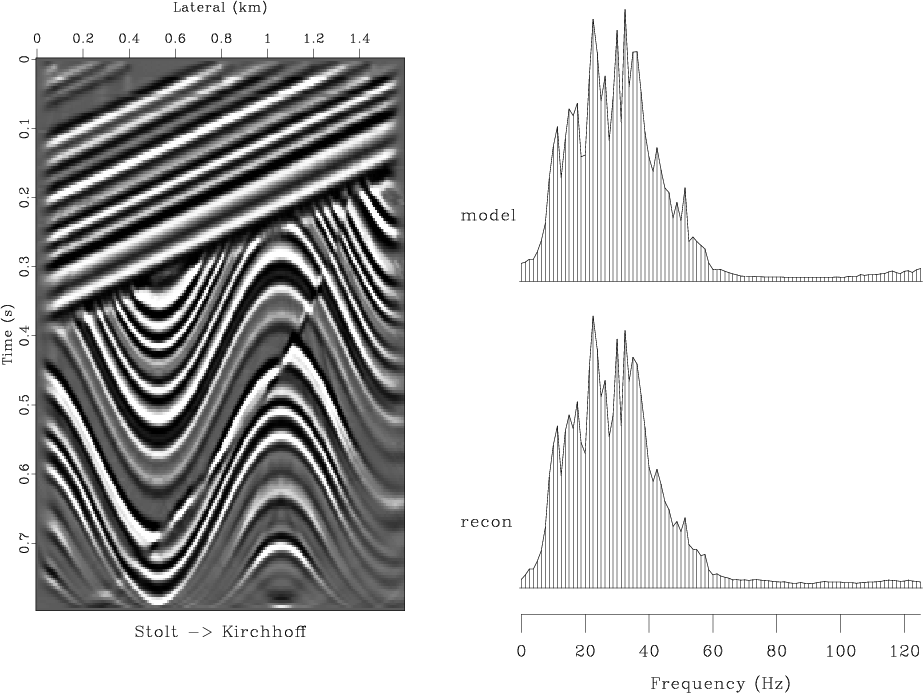
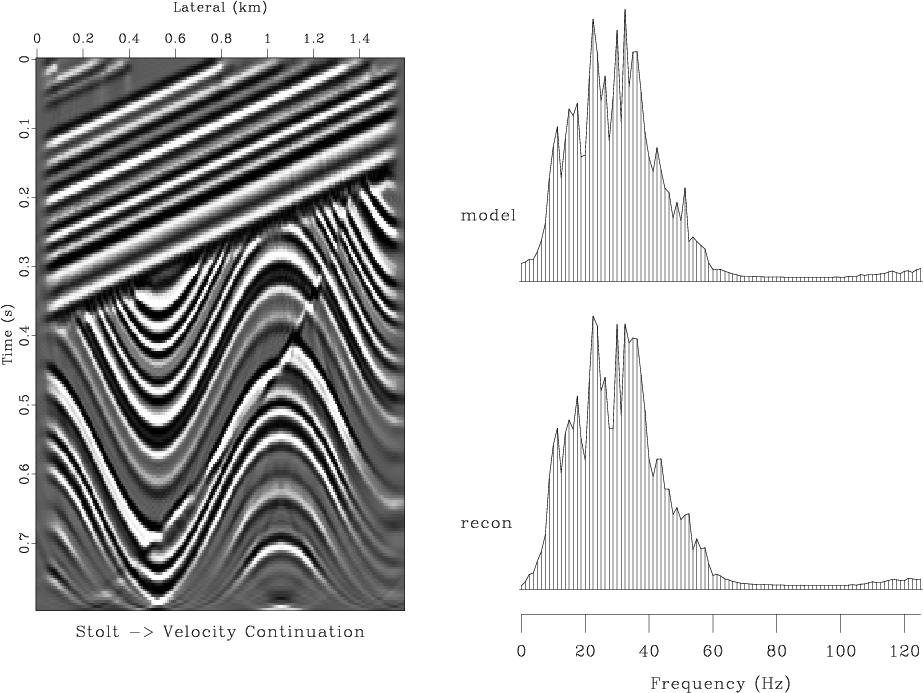
of velocity continuation, shown in Figure 6, is
noticeably more accurate than that of the Kirchhoff method.
(Stolt, 1978) methods, respectively. These figures should
be compared with Figure 5, showing the analogous result
of the finite-difference velocity continuation. The comparison
reveals a remarkable invertability of velocity continuation, which
reconstructs accurately the main features and frequency content of the
model. Since the forward operators were different for different
migrations, this comparison did not test the migration properties
themselves. For such a test, I compare the results of the Kirchhoff
and velocity-continuation migrations after Stolt modeling. The result
of velocity continuation, shown in Figure 6, is
noticeably more accurate than that of the Kirchhoff method.
|
|---|
|
vlckaa
Figure 3. Result of modeling and migration with the Kirchhoff method. Top left plot shows the reconstructed model. Top right plot compares the average amplitude spectrum of the true model with that of the reconstructed image. Bottom left is the reconstruction error. Bottom right is the absolute error in the spectrum. |
|
|
|
|---|
|
vlcsto
Figure 4. Result of modeling and migration with the Stolt method. Top left plot shows the reconstructed model. Top right plot compares the average amplitude spectrum of the true model with that of the reconstructed image. Bottom left is the reconstruction error. Bottom right is the absolute error in the spectrum. |
|
|
|
|---|
|
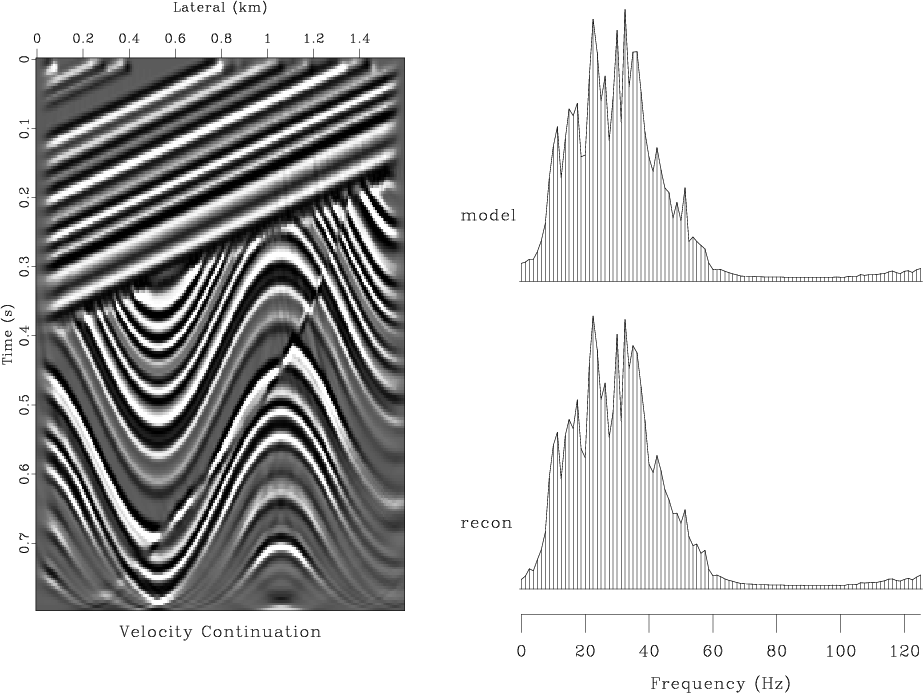
vlcvel
Figure 5. Result of modeling and migration with the finite-difference velocity continuation. Top left plot shows the reconstructed model. Top right plot compares the average amplitude spectrum of the true model with that of the reconstructed image. Bottom left is the reconstruction error. Bottom right is the absolute error in the spectrum. |
|
|
|
|---|
|
vlcstk,vlcstv
Figure 6. (a) Modeling with Stolt method, migration with the Kirchhoff method. (b) Modeling with Stolt method, migration with the finite-difference velocity continuation. Left plots show the reconstructed models. Right plots show the reconstruction errors. |
|
|
These tests confirm that finite-difference velocity continuation is an attractive migration method. It possesses remarkable invertability properties, which may be useful in applications that require inversion. While the traditional migration methods transform the data between two completely different domains (data-space and image-space), velocity continuation accomplishes the same transformation by propagating the data in the extended domain along the velocity direction. Inverse propagation restores the original data. According to Li (1986), the computational speed of this method compares favorably with that of Stolt migration. The advantage is apparent for cascaded migration or migration with multiple velocity models. In these cases, the cost of Stolt migration increases in direct proportion to the number of velocity models, while the cost of velocity continuation stays the same.
|
|
|
|
Time migration velocity analysis by velocity continuation |