|
|
|
|
Velocity continuation and the anatomy of residual prestack time migration |
The derivation of the residual DMO+NMO kinematics is detailed in Appendix B. Figure 5 illustrates it with the theoretical impulse response curves. Figure 6 compares the theoretical curves with the result of an actual cascade of the inverse DMO, residual NMO, and DMO operators.
|
|---|
|
vlcvcp
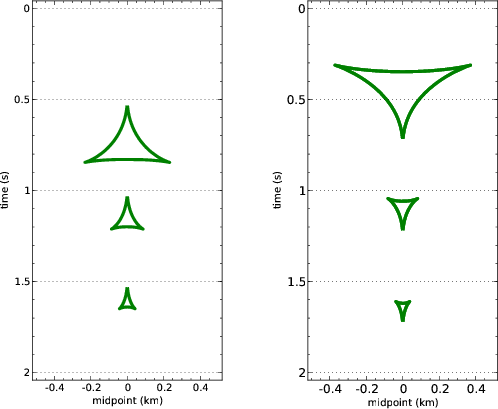
Figure 5. Theoretical kinematics of the residual NMO+DMO impulse responses for three impulses. Left plot: the velocity ratio |
|
|
|
|---|
|
vlccps
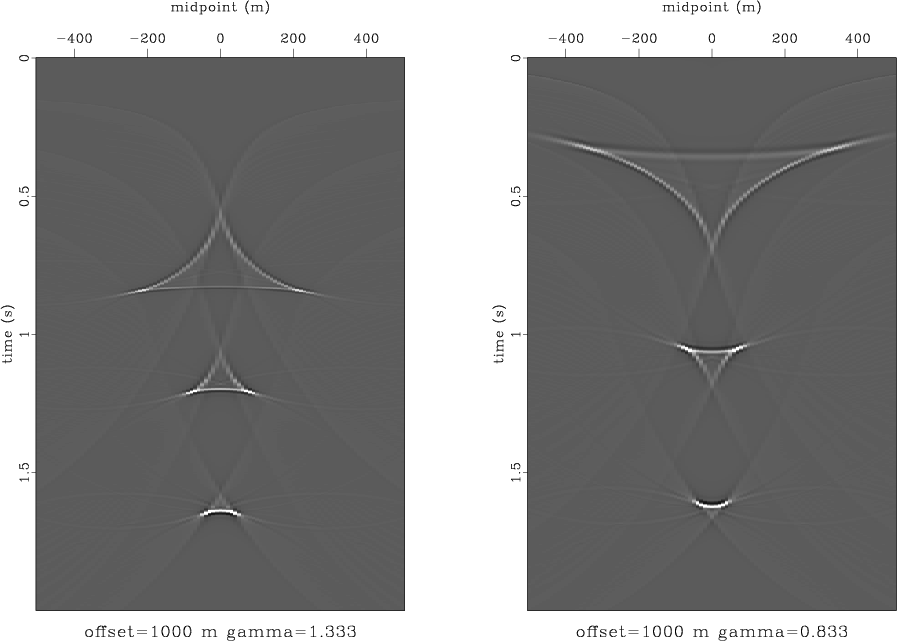
Figure 6. The result of residual NMO+DMO (cascading inverse DMO, residual NMO, and DMO) for three impulses. Left plot: the velocity ratio |
|
|
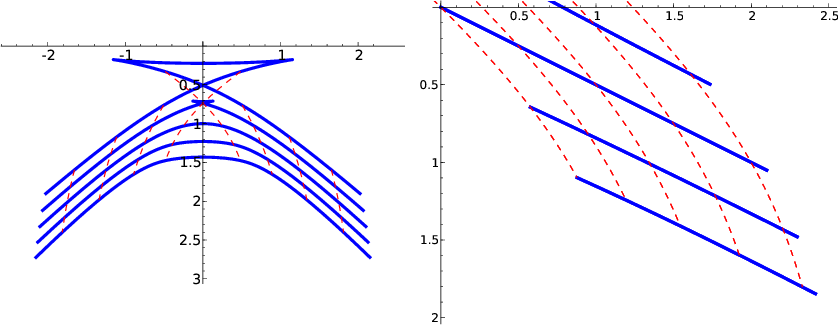
Figure 7 illustrates the residual NMO+DMO velocity continuation for two particularly interesting cases. The left plot shows the continuation for a point diffractor. One can see that when the velocity error is large, focusing of the velocity rays forms a distinctive loop on the zero-offset hyperbola. The right plot illustrates the case of a plane dipping reflector. The image of the reflector shifts both vertically and laterally with the change in NMO velocity.
|
|---|
|
vlcvrd
Figure 7. Kinematic velocity continuation for residual NMO+DMO. Solid lines denote wavefronts: zero-offset traveltime curves; dashed lines denote velocity rays. a: the case of a point diffractor; the velocity ratio |
|
|
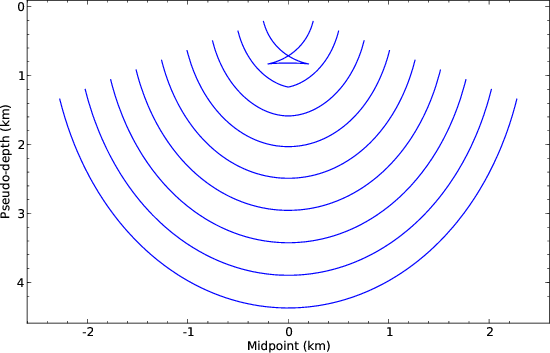
The full residual migration operator is the chain of
residual zero-offset migration and residual NMO+DMO. I illustrate the
kinematics of this operator in Figures 8 and 9,
which are designed to match Etgen's Figures 2.4 and 2.5
(Etgen, 1990). A comparison with Figures 3 and
4 shows that including the residual DMO term affects
the images of objects with the depth smaller than the half-offset
![]() . This term complicates the residual migration operator with cusps.
. This term complicates the residual migration operator with cusps.
|
vlcve3
Figure 8. Summation paths of prestack residual migration for a series of depth diffractors. Residual slowness |
|
|---|---|
|
|
|
vlcve4
Figure 9. Summation paths of prestack residual migration for a series of depth diffractors. Residual slowness |

|
|---|---|
|
|
|
|
|
|
Velocity continuation and the anatomy of residual prestack time migration |