 |
 |
 |
 | Velocity continuation and the anatomy of
residual prestack time migration |  |
![[pdf]](icons/pdf.png) |
Next: Kinematics of Residual DMO
Up: KINEMATICS OF VELOCITY CONTINUATION
Previous: Kinematics of Zero-Offset Velocity
The residual NMO differential equation is the second term in
equation (1):
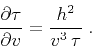 |
(22) |
Equation (22) does not depend on the midpoint
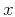 . This fact indicates the one-dimensional nature of normal
moveout. The general solution of equation (22) is
obtained by simple integration. It takes the form
. This fact indicates the one-dimensional nature of normal
moveout. The general solution of equation (22) is
obtained by simple integration. It takes the form
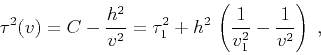 |
(23) |
where 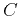 is an arbitrary velocity-independent constant, and I have chosen the
constants
is an arbitrary velocity-independent constant, and I have chosen the
constants 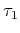 and
and 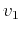 so that
so that
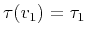 .
Equation (23) is applicable only for
.
Equation (23) is applicable only for 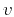 different from zero.
different from zero.
For the case of a point diffractor, equation (23) easily
combines with the zero-offset solution (16). The result
is a simplified approximate version of the prestack residual migration
summation path:
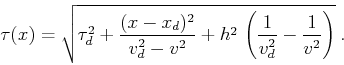 |
(24) |
Summation paths of the form (24) for a set of diffractors
with different depths are plotted in Figures 3 and
4. The parameters chosen in these plots allow a direct
comparison with Etgen's Figures 2.4 and 2.5 (Etgen, 1990),
based on the exact solution and reproduced in Figures 8 and
9. The comparison shows that the approximate
solution (24) captures the main features of the prestack
residual migration operator, except for the residual DMO cusps
appearing in the exact solution when the diffractor depth is smaller
than the offset.
vlcve1
Figure 3. Summation paths of the simplified
prestack residual migration for a series of depth diffractors.
Residual slowness 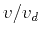 is 1.2; half-offset is 1.2; half-offset 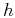 is 1 km. This
figure is to be compared with Etgen's Figure 2.4, reproduced in
Figure 8. is 1 km. This
figure is to be compared with Etgen's Figure 2.4, reproduced in
Figure 8.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[sage]](icons/sage.png)
|
|---|
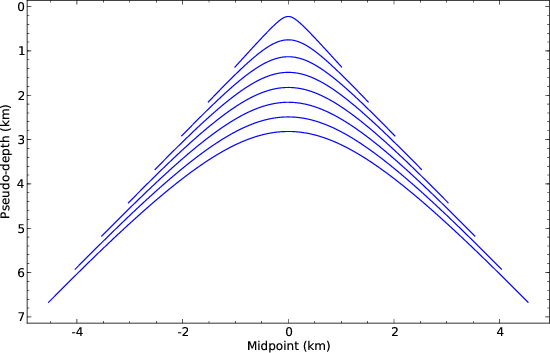
vlcve2
Figure 4. Summation paths of the simplified
prestack residual migration for a series of depth diffractors.
Residual slowness 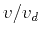 is 0.8; offset is 0.8; offset 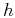 is 1 km. This figure is
to be compared with Etgen's Figure 2.5, reproduced in
Figure 9. is 1 km. This figure is
to be compared with Etgen's Figure 2.5, reproduced in
Figure 9.
|
|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[sage]](icons/sage.png)
|
|---|
Neglecting the residual DMO term in residual migration is
approximately equivalent in accuracy to neglecting the DMO step in
conventional processing. Indeed, as follows from the geometric analog
of equation (1) derived in Appendix A
[equation (A-17)], dropping the residual
DMO term corresponds to the condition
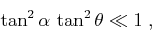 |
(25) |
where  is the dip angle, and
is the dip angle, and 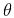 is the reflection angle.
As shown by Yilmaz and Claerbout (1980), the conventional processing
sequence without the DMO step corresponds to the separable
approximation of the double-square-root equation (A-4):
is the reflection angle.
As shown by Yilmaz and Claerbout (1980), the conventional processing
sequence without the DMO step corresponds to the separable
approximation of the double-square-root equation (A-4):
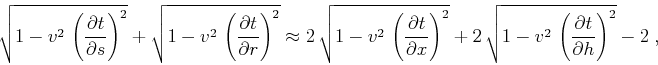 |
(26) |
where 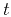 is the reflection traveltime, and
is the reflection traveltime, and 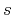 and
and 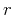 are the source and
receiver coordinates:
are the source and
receiver coordinates:  ,
, 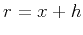 .
In geometric terms, approximation (26) transforms to
.
In geometric terms, approximation (26) transforms to
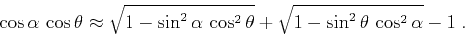 |
(27) |
Taking the difference of the two sides of
equation (27), one can estimate its accuracy by the
first term of the Taylor series for small  and
and 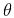 . The
estimate is
. The
estimate is
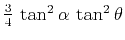 (Yilmaz and Claerbout, 1980), which agrees qualitatively with
(25). Although approximation (24) fails in situations
where the dip moveout correction is necessary, it is significantly
more accurate than the 15-degree approximation of the
double-square-root equation, implied in the migration velocity
analysis method of Yilmaz and Chambers (1984) and MacKay and Abma (1992). The
15-degree approximation
(Yilmaz and Claerbout, 1980), which agrees qualitatively with
(25). Although approximation (24) fails in situations
where the dip moveout correction is necessary, it is significantly
more accurate than the 15-degree approximation of the
double-square-root equation, implied in the migration velocity
analysis method of Yilmaz and Chambers (1984) and MacKay and Abma (1992). The
15-degree approximation
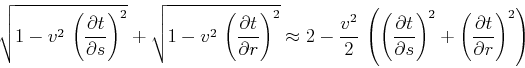 |
(28) |
corresponds geometrically to the equation
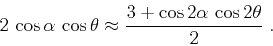 |
(29) |
Its estimated accuracy (from the first term of the Taylor series)
is
 . Unlike the separable approximation, which is
accurate separately for zero offset and zero dip, the 15-degree
approximation fails at zero offset in the case of a steep dip and at zero
dip in the case of a large offset.
. Unlike the separable approximation, which is
accurate separately for zero offset and zero dip, the 15-degree
approximation fails at zero offset in the case of a steep dip and at zero
dip in the case of a large offset.
 |
 |
 |
 | Velocity continuation and the anatomy of
residual prestack time migration |  |
![[pdf]](icons/pdf.png) |
Next: Kinematics of Residual DMO
Up: KINEMATICS OF VELOCITY CONTINUATION
Previous: Kinematics of Zero-Offset Velocity
2014-04-01

