 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: 2. Zero-offset migration
Up: Migration
Previous: Migration
In the case of common-shot migration, we can simplify equation (46)
with the help of Gritsenko's formula (35) to the form
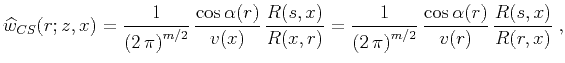 |
(48) |
where the angle 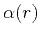 is measured between the reflected ray and
the normal to the observation surface at the reflector point
is measured between the reflected ray and
the normal to the observation surface at the reflector point  .
Formula (48) coincides with the analogous result of
Keho and Beydoun (1988), derived directly from Claerbout's imaging
principle (Claerbout, 1970). An alternative derivation is
given by Goldin (1987). Docherty (1991) points out a
remarkable correspondence between this formula and the classic results
of Born scattering inversion (Bleistein, 1987).
.
Formula (48) coincides with the analogous result of
Keho and Beydoun (1988), derived directly from Claerbout's imaging
principle (Claerbout, 1970). An alternative derivation is
given by Goldin (1987). Docherty (1991) points out a
remarkable correspondence between this formula and the classic results
of Born scattering inversion (Bleistein, 1987).
For common-shot migration, pseudo-unitary weighting coincides with the
weighting of datuming and corresponds to the downward continuation of the
receivers.
2013-03-03