Antialiasing of Kirchhoff operators by reciprocal parameterization

Hale's method

Considering the case of integral dip moveout, Hale (1991) points out that the steep parts of the operator, while aliased in the space (midpoint) coordinate, are not aliased with respect to the time coordinate. He suggests replacing the conventional $t(x)$ parameterization of the DMO impulse response by $x(t)$ parameterization. Conventionally, the integral operators are implemented by shifting the input traces in space and transforming them in time. According to Hale's method, the traces are shifted in time and transformed along the $x(t)$ trajectories in space. Interpolation in time, required in the conventional approach, is replaced by interpolation in space. The idea of Hale's method is related to the idea of the ``pixel-precise velocity transform'' (Claerbout, 1992b).

The steep parts of the operator satisfy the criterion

$$\Delta t \leq {{\Delta x} \over {\vert\partial x / \partial t\vert}}\;,$$ (4)

which is the the obvious reverse of inequality (1). Therefore, they are not aliased if defined on the time grid. In these parts, one can implement the operator by constant time shifts equal to the time sampling interval $\Delta t$. In the parts where the criterion (4) is not valid (the flat part of the DMO operator), Hale suggests reducing the length of the time shifts according to equality (2), where $\delta t$ becomes less than $\Delta t$. He formulates the following principle of operator antialiasing:

To eliminate spatial aliasing, simply never allow successive time shifts applied to the input trace to differ by more than one time sampling interval. Further restrict the difference between time shifts so that the spacing between the corresponding output trajectories never exceeds the CMP sampling interval.

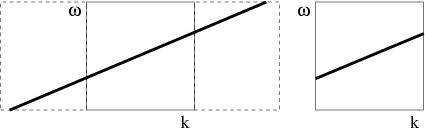
The idea of Hale's method is illustrated in Figure 3. Increasing the density of spatial sampling by small successive time shifts implies increasing the Nyquist boundaries of the spatial wavenumber. Further interpolation is a low-pass spatial filtering that removes the parts of the spectrum beyond the Nyquist frequency of the output. If the dip of the operator does not vary between neighboring traces (the operator is a straight line as in the slant stack case), Hale's approach will produce essentially the same result as that of temporal filtering. Triangle filters in this case approximately correspond to linear interpolation in space between adjacent traces (Nichols, 1993). The difference between the two approaches occurs if the local dip varies in space as in the case of a curved operator, such as DMO. In this case, Hale's approach provides a more accurate space interpolation of the operator and preserves the high-frequency part of its spectrum from distortion.

amosft
Figure 3. Schematic illustration of Hale's antialiasing. The aliased events are removed by spatial interpolation. In the frequency domain, the interpolation consists of widening and low-passing on the wavenumber axis. The low-pass spatial filtering does not depend on dip.

Hale's method has proven to preserve the amplitude of flat reflectors from aliasing distortions, which is the simplest antialiasing test on a DMO operator. The most valuable advantage of this method in the fact that the implied low-pass spatial filtering (interpolation) does not depend on the operator dip and is controlled by the Nyquist boundary of the spectrum only (compare Figures 1 and 3). This is especially important, when the local dip of the operator changes rapidly and therefore cannot be estimated precisely by finite-difference approximation at spatially separated traces. Such a situation is common in dip moveout and azimuth moveout integral operators, as well as in prestack Kirchhoff migration.

A weakness of the method is the necessity to switch from interpolation in space to two-dimensional interpolation in both the time and the space variables, when trying to construct the flat part of the operator. In the next section, I show how to avoid the expense of the additional time interpolation required by Hale's method of antialiasing.

Antialiasing of Kirchhoff operators by reciprocal parameterization