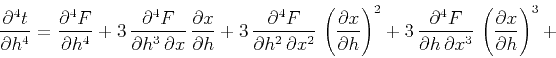|
 |
 |
 | Nonhyperbolic reflection moveout of 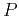 -waves:
An overview and comparison of reasons -waves:
An overview and comparison of reasons |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Fomel & Grechka: Nonhyperbolic
Previous: Conclusions
This paper is the result of a year-long email correspondence. Its
outline was created when the first author visited Colorado
School of Mines. We acknowledge the support of the Stanford
Exploration Project and the Center for Wave Phenomena (CWP) Consortium
Project. The second author was also supported by the United States
Department of Energy (Award #DE-FG03-98ER14908). We thank Ken Larner
and Petr Jílek for reviewing the manuscript, and Ilya Tsvankin
and other members of the A(nisotropy)-team for insightful discussions.
Appendix
A
NORMAL MOVEOUT BEYOND THE NIP THEOREM
In this Appendix, we derive equations that relate traveltime
derivatives of the reflected wave, evaluated at the zero offset point,
and traveltime derivatives of the direct wave, evaluated in the
vicinity of the zero-offset ray. Such a relationship for second-order
derivatives is known as the NIP (normal incidence point) theorem
(Hubral, 1983; Chernjak and Gritsenko, 1979; Hubral and Krey, 1980). Its extension to high-order
derivatives is described by Fomel (1994).
Reflection traveltime in any type of model can be considered as a
function of the source and receiver locations  and
and 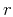 and the
location of the reflection point
and the
location of the reflection point  , as follows:
, as follows:
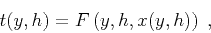 |
(83) |
where 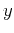 is the midpoint
is the midpoint
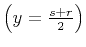 ,
, 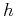 is
the half-offset
is
the half-offset
 , and the
function
, and the
function 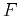 has a natural decomposition into two parts corresponding
to the incident and reflected rays:
has a natural decomposition into two parts corresponding
to the incident and reflected rays:
 |
(84) |
where  is the traveltime of the direct wave. Clearly, at the
zero-offset point,
is the traveltime of the direct wave. Clearly, at the
zero-offset point,
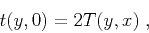 |
(85) |
where  corresponds to the reflection point of the
zero-offset ray.
corresponds to the reflection point of the
zero-offset ray.
Differentiating equation (K-1) with respect to the half-offset
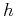 and applying the chain rule, we obtain
and applying the chain rule, we obtain
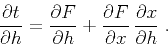 |
(86) |
According to Fermat's principle, one of the
fundamental principles of ray theory, the ray
trajectory of the reflected wave corresponds to an
extremum value of the traveltime. Parameterizing
the trajectory in terms of the reflection point
location  and assuming that
and assuming that 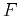 is a smooth
function of
is a smooth
function of  , we can write Fermat's principle
in the form
, we can write Fermat's principle
in the form
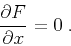 |
(87) |
Equation (K-5) must be satisfied for any values of  and
and
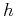 . Substituting this equation into equation (K-4) leads to the
equation
. Substituting this equation into equation (K-4) leads to the
equation
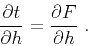 |
(88) |
Differentiating (K-6) again with respect to 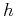 , we arrive at the
equation
, we arrive at the
equation
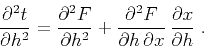 |
(89) |
Interchanging the source and receiver locations doesn't change the
reflection point position (the principle of reciprocity). Therefore,
 is an even function of the offset
is an even function of the offset 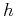 , and we can simplify equation
(K-7) at zero offset, as follows:
, and we can simplify equation
(K-7) at zero offset, as follows:
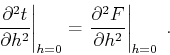 |
(90) |
Substituting the expression for the function 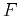 (K-2) into
(K-8) leads to the equation
(K-2) into
(K-8) leads to the equation
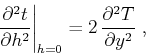 |
(91) |
which is the mathematical formulation of the NIP theorem. It proves
that the second-order derivative of the reflection traveltime with
respect to the offset is equal, at zero offset, to the second
derivative of the direct wave traveltime for the wave propagating from
the incidence point of the zero-offset ray. One immediate conclusion
from the NIP theorem is that the short-spread normal moveout velocity,
connected with the derivative in the left-hand-side of equation
(K-9) can depend on the reflector dip but doesn't depend on
the curvature of the reflector. Our derivation up to this point has
followed the derivation suggested by Chernjak and Gritsenko (1979).
Differentiating equation (K-7) twice with respect to 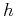 evaluates,
with the help of the chain rule, the fourth-order derivative, as
follows:
evaluates,
with the help of the chain rule, the fourth-order derivative, as
follows:
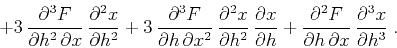 |
(92) |
Again, we can apply the principle of reciprocity to eliminate the
odd-order derivatives of  in equation (K-10) at the zero
offset. The resultant expression has the form
in equation (K-10) at the zero
offset. The resultant expression has the form
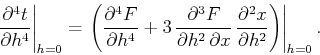 |
(93) |
In order to determine the unknown second derivative of the reflection
point location
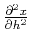 , we
differentiate Fermat's equation (K-5) twice, obtaining
, we
differentiate Fermat's equation (K-5) twice, obtaining
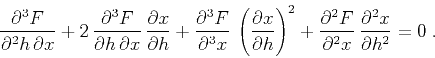 |
(94) |
Simplifying this equation at zero offset, we can solve it for the
second derivative of  . The solution has the form
. The solution has the form
![\begin{displaymath}
\left.{{\partial^2 x} \over {\partial h^2}}\right\vert _{h=0...
...partial^3 F} \over {\partial^2 h \partial x}}\right]_{h=0}\;.
\end{displaymath}](img208.png) |
(95) |
Here we neglect the case of
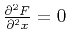 , which corresponds to a focusing of the reflected rays at the
surface. Finally, substituting expression (K-13) into (K-11)
and recalling the definition of the
, which corresponds to a focusing of the reflected rays at the
surface. Finally, substituting expression (K-13) into (K-11)
and recalling the definition of the 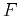 function
from (K-2), we obtain
the equation
function
from (K-2), we obtain
the equation
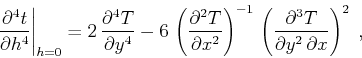 |
(96) |
which is the same as equation (67) in the main
text. Higher-order derivatives can be expressed in an analogous way
with a set of recursive algebraic functions (Fomel, 1994).
In the derivation of equations (K-9) and (K-14),
we have used Fermat's principle, the principle of reciprocity, and the
rules of calculus. Both these equations remain valid in anisotropic
media as well as in heterogeneous media, providing that the traveltime
function is smooth and that focusing of the reflected rays doesn't
occur at the surface of observation.
 |
 |
 |
 | Nonhyperbolic reflection moveout of  -waves:
An overview and comparison of reasons -waves:
An overview and comparison of reasons |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Fomel & Grechka: Nonhyperbolic
Previous: Conclusions
2013-03-03
![]() and
and ![]() and the
location of the reflection point
and the
location of the reflection point ![]() , as follows:
, as follows:
![]() and applying the chain rule, we obtain
and applying the chain rule, we obtain
![]() , we arrive at the
equation
, we arrive at the
equation
![]() evaluates,
with the help of the chain rule, the fourth-order derivative, as
follows:
evaluates,
with the help of the chain rule, the fourth-order derivative, as
follows: