|
|
|
|
Madagascar tutorial |
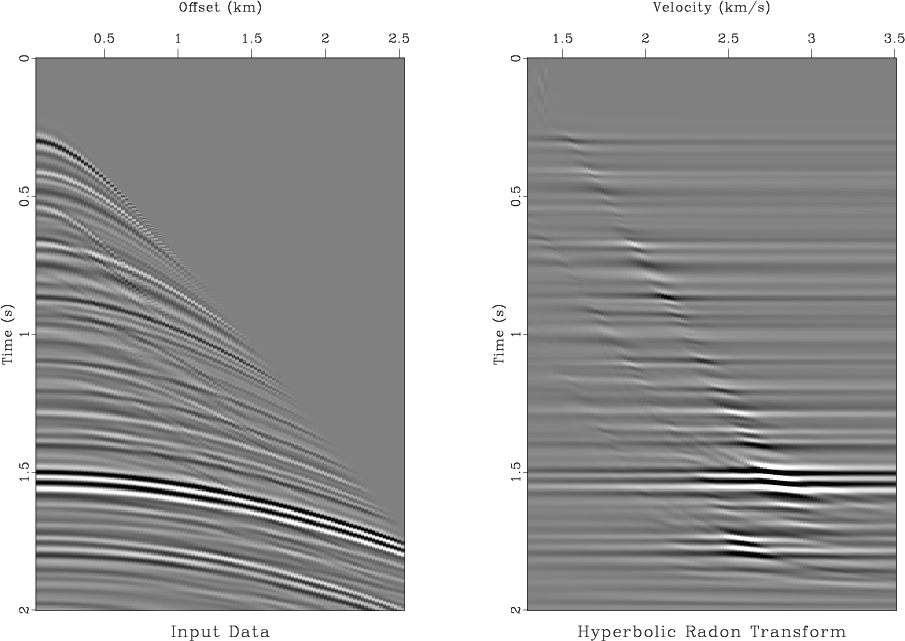
Next, we will apply the hyperbolic Radon transform (also known as the velocity stack or the velocity transform) to our modeled CMP gather in order to separate primaries and multiples. As suggested by Thorson and Claerbout (1985), the hyperbolic Radon transform can be made invertible by employing an iterative least-squares inversion.
|
|---|
|
radon
Figure 4. Synthetic CMP gather (left) its hyperbolic Radon transform (right). |
|
|
bash$ scons radon.view
To test if the adjoint operator is implemented correctly in this program, you can run the dot-product test
bash$ sfdottest ./hradon.exe mod=radon.rsf dat=cmp2.rsf \ ov=1.3 dv=0.02 nv=111 ox=0.05 dx=0.025 nx=100The output should display a pair of numbers equal to six digits of accuracy. You can run the test multiple times.
The result of going back from the Radon domain to the CMP domain using the adjoint operation is shown in Figure 5a. To display it on your screen, run
bash$ scons adj.view


|
|---|
|
adj,inv
Figure 5. Synthetic CMP gather reconstructed from the inverse transform (left) and its difference wit the original gather (right). Top: using adjoint transform, bottom: using 10 iterations of iterative least-squares inversion. |
|
|
bash$ scons inv.view
Notice that only 10 conjugate-gradient iterations are sufficient to achieve a reasonable reconstruction.
Open the hradon.c program in an editor and uncomment the lines containing calls to halfint_lop (the half-order derivative filter for correcting the wavelet shape). Replace XXXX with true or false as appropriate and comment out extra calls to sf_floatread and sf_floatwrite. To check if you did it correctly, run the dot-product test
bash$ sfdottest ./hradon.exe mod=radon.rsf dat=cmp2.rsf \ ov=1.3 dv=0.02 nv=111 ox=0.05 dx=0.025 nx=100Did including the half-order derivative filter improve the convergence of conjugate gradients?
You can try to achieve a further acceleration using preconditioning by diagonal weighting. Appropriate weights can be found by experimentation or by using the asymptotic theory (Fomel, 2003).
scons mute.view mult.viewVerify that the separated primaries and multiples sum to the original CMP gather (check out the sfadd program.)
To confirm the separation, we can also run the semblance scan on the separated results (Figure 7b.) To display it on your screen, run
scons vscan.view

|
|---|
|
mute
Figure 6. Isolating signal in the hyperbolic Radon domain (left) by muting (right). |
|
|


|
|---|
|
mult,vscan
Figure 7. (a) Separated primaries and multiples. (b) Velocity analysis using semblance scan applied to separated primaries and multiples. |
|
|
/* Hyperbolic Radon transform */
#include <rsf.h>
int main(int argc, char* argv[])
{
sf_map4 map;
int it,nt, ix,nx, iv,nv, i3,n3;
bool adj;
float t0,dt,t, x0,dx,x, v0,dv,v;
float **cmp, **rad, *trace;
sf_file in, out;
/* initialize Madagascae */
sf_init(argc,argv);
/* input and output files */
in = sf_input("in");
out = sf_output("out");
/* Time axis parameters from the input */
if (!sf_histint(in,"n1",&nt)) sf_error("No n1=");
if (!sf_histfloat(in,"o1",&t0)) sf_error("No o1=");
if (!sf_histfloat(in,"d1",&dt)) sf_error("No d1=");
/* number of CMPS */
n3 = sf_leftsize(in,2);
if (!sf_getbool("adj",&adj)) adj=false;
/* adjoint flag */
if (adj) {
if (!sf_histint(in,"n2",&nx)) sf_error("No n2=");
if (!sf_histfloat(in,"o2",&x0)) sf_error("No o2=");
if (!sf_histfloat(in,"d2",&dx)) sf_error("No d2=");
if (!sf_getint("nv",&nv)) sf_error("Need nv=");
if (!sf_getfloat("ov",&v0)) sf_error("need ov=");
if (!sf_getfloat("dv",&dv)) sf_error("need dv=");
sf_putint(out,"n2",nv);
sf_putfloat(out,"o2",v0);
sf_putfloat(out,"d2",dv);
sf_putstring(out,"label2","Velocity");
sf_putstring(out,"unit2","km/s");
} else {
if (!sf_histint(in,"n2",&nv)) sf_error("No n2=");
if (!sf_histfloat(in,"o2",&v0)) sf_error("No o2=");
if (!sf_histfloat(in,"d2",&dv)) sf_error("No d2=");
if (!sf_getint("nx",&nx)) sf_error("Need nx=");
if (!sf_getfloat("ox",&x0)) sf_error("need ox=");
if (!sf_getfloat("dx",&dx)) sf_error("need dx=");
sf_putint(out,"n2",nx);
sf_putfloat(out,"o2",x0);
sf_putfloat(out,"d2",dx);
sf_putstring(out,"label2","Offset");
sf_putstring(out,"unit2","km");
}
/* allocate storage */
trace = sf_floatalloc(nt);
rad = sf_floatalloc2(nt,nv);
cmp = sf_floatalloc2(nt,nx);
/* initialize half-order differentiation */
sf_halfint_init (true,nt,1.0f-1.0f/nt);
/* initialize spline interpolation */
map = sf_stretch4_init (nt, t0, dt, nt, 0.01);
for (i3=0; i3 < n3; i3++) {
if( adj) {
/*
for (ix=0; ix < nx; ix++) {
sf_floatread(trace,nt,in);
sf_halfint_lop(XXXX,false,nt,nt,cmp[ix],trace);
}
*/
sf_floatread(cmp[0],nt*nx,in);
} else {
sf_floatread(rad[0],nt*nv,in);
}
/* zero output */
sf_adjnull(adj,false,nt*nv,nt*nx,rad[0],cmp[0]);
for (iv=0; iv < nv; iv++) {
v = v0 + iv*dv;
for (ix=0; ix < nx; ix++) {
x = (x0 + ix*dx)/v;
for (it=0; it < nt; it++) {
t = t0 + it*dt;
trace[it] = hypotf(t,x);
/* hypot(a,b)=sqrt(a*a+b*b) */
}
/* define mapping */
sf_stretch4_define(map,trace);
if (adj) {
sf_stretch4_apply_adj(true,map,rad[iv],cmp[ix]);
} else {
sf_stretch4_apply (true,map,rad[iv],cmp[ix]);
}
}
}
if (adj) {
sf_floatwrite(rad[0],nt*nv,out);
} else {
sf_floatwrite(cmp[0],nt*nx,out);
/*
for (ix=0; ix < nx; ix++) {
sf_halfint_lop(XXXX,false,nt,nt,cmp[ix],trace);
sf_floatwrite(trace,nt,out);
}
*/
}
}
exit(0);
}
|
from rsf.proj import *
# Use cmp2 data from the previous project
Fetch('cmp2.rsf','synth',top='..',server='local')
Plot('cmp2','grey title="Input Data" clip=6')
# Compile hyperbolic Radon program
prog = Program('hradon.c')
hradon = str(prog[0])
# Hyperbolic Radon using adjoint
################################
Flow('radon',['cmp2',hradon],
'${SOURCES[1].abspath} adj=y ov=1.3 dv=0.02 nv=111')
Plot('radon',
'grey title="Hyperbolic Radon Transform" ')
Result('radon','cmp2 radon','SideBySideAniso')
Flow('adj',['radon',hradon],
'${SOURCES[1].abspath} ox=0.05 dx=0.025 nx=100')
Plot('adj',
'grey title="Adjoint Hyperbolic Radon Transform" ')
Flow('adiff','cmp2 adj','add scale=1,-1 ${SOURCES[1]}')
Plot('adiff','grey title=Difference clip=6')
Result('adj','adj adiff','SideBySideAniso')
# Hyperbolic Radon using least-squares inversion
################################################
Flow('radon2',['cmp2',hradon,'radon'],
'''
conjgrad ${SOURCES[1].abspath} mod=${SOURCES[2]}
ov=1.3 dv=0.02 nv=111 ox=0.05 dx=0.025 nx=100 niter=10
''')
Plot('radon2',
'grey title="Hyperbolic Radon Transform" ')
Flow('inv',['radon2',hradon],
'${SOURCES[1].abspath} ox=0.05 dx=0.025 nx=100')
Plot('inv',
'grey title="Inverse Hyperbolic Radon Transform" clip=6')
Flow('idiff','cmp2 inv','add scale=1,-1 ${SOURCES[1]}')
Plot('idiff','grey title=Difference clip=6')
Result('inv','inv idiff','SideBySideAniso')
# Separating primaries and multiples
####################################
Flow('mute','radon2',
'mutter half=n t0=0.48 x0=1.5 v0=1 inner=y')
Plot('mute','grey title="Muted Multiples" ')
Result('mute','radon2 mute','SideBySideAniso')
Flow('prim',['mute',hradon],
'${SOURCES[1].abspath} ox=0.05 dx=0.025 nx=100')
Plot('prim',
'grey title="Estimated Primaries" clip=6')
Flow('mult','cmp2 prim','add scale=1,-1 ${SOURCES[1]}')
Plot('mult','grey title="Estimated Multiples" clip=6')
Result('mult','prim mult','SideBySideAniso')
# Velocity analysis
###################
Flow('pvscan','prim',
'vscan half=n v0=1.5 nv=101 dv=0.02 semblance=y')
Plot('pvscan',
'''
grey color=j allpos=y title="Primaries Semblance Scan"
''')
Flow('mvscan','mult',
'vscan half=n v0=1.5 nv=101 dv=0.02 semblance=y')
Plot('mvscan',
'''
grey color=j allpos=y title="Multiples Semblance Scan"
''')
Result('vscan','pvscan mvscan','SideBySideAniso')
End()
|
|
|
|
|
Madagascar tutorial |