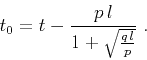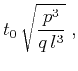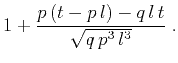|
 |
 |
 | Velocity-independent time-domain seismic imaging
using
local event slopes |  |
![[pdf]](icons/pdf.png) |
Next: Dix inversion
Up: Oriented time-domain imaging
Previous: - NMO
The hyperbolic model 1 is not accurate at large offsets in the
case of non-hyperbolic moveouts, caused by vertical or lateral heterogeneity,
reflector curvature, or anisotropy (Fomel and Grechka, 2001). One popular model for
describing non-hyperbolic moveouts was developed by Malovichko (1978) and has the
form of a shifted hyperbola
(de Bazelaire, 1988; Castle, 1994; Siliqi and Bousquié, 2000)
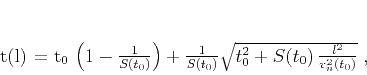 |
(9) |
Equation 9 contains an additional parameter 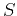 , which
is related to heterogeneity and anisotropy of seismic velocities. We
can eliminate this parameter by differentiating the equation twice and
defining the second derivative
, which
is related to heterogeneity and anisotropy of seismic velocities. We
can eliminate this parameter by differentiating the equation twice and
defining the second derivative
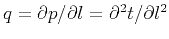 .
Eliminating both
.
Eliminating both 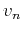 and
and 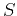 from equation 9 and equations
from equation 9 and equations
leads to the
velocity-independent non-hyperbolic moveout equation
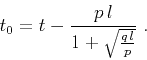 |
(12) |
If moveout parameters 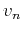 and
and 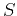 are required for subsequent
interpretation, one can easily extract them as special data attributes
are required for subsequent
interpretation, one can easily extract them as special data attributes
One could estimate the function 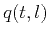 in practice by numerically
differentiating the local slope field
in practice by numerically
differentiating the local slope field 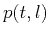 .
.
 |
 |
 |
 | Velocity-independent time-domain seismic imaging
using
local event slopes |  |
![[pdf]](icons/pdf.png) |
Next: Dix inversion
Up: Oriented time-domain imaging
Previous: - NMO
2013-03-02