 |
 |
 |
 | Accelerated plane-wave destruction |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Chen, Fomel & Lu:
Previous: Acknowledgments
If all the coefficients of 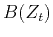 are polynomials of
are polynomials of 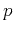 ,
equation 4 is also a polynomial of
,
equation 4 is also a polynomial of 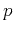 ,
and the plane-wave destruction equation becomes
in turn a polynomial equation of
,
and the plane-wave destruction equation becomes
in turn a polynomial equation of 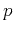 .
The problem is to design a
.
The problem is to design a 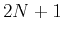 points filter
points filter 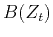 with polynomial coefficients
such that the allpass system
with polynomial coefficients
such that the allpass system
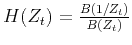 can approximate
the phase-shift operator
can approximate
the phase-shift operator
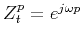 .
Denoting the phase response of the system as
.
Denoting the phase response of the system as
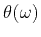 ,
that is
,
that is
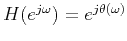 ,
the group delay of the system is
,
the group delay of the system is
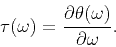 |
(24) |
The maximally flat criteria designs a filter
with a smoothest phase response.
There are 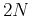 unknown coefficients in
unknown coefficients in 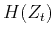 ,
so we can add
,
so we can add 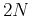 flat constraints for the first
flat constraints for the first 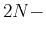 th order deviratives
of the phase response.
It becomes
(Zhang, 2009, equation 7)
th order deviratives
of the phase response.
It becomes
(Zhang, 2009, equation 7)
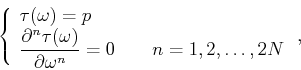 |
(25) |
which is equivalent to the following linear maximally flat conditions
(Thiran, 1971):
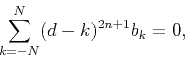 |
(26) |
where
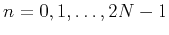 and
and
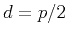 is the fractional delay of
is the fractional delay of 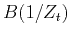 or
or 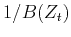 .
.
In order to solve 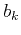 from the above equations,
Thiran (1971) used an additional condition
from the above equations,
Thiran (1971) used an additional condition 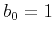 ,
which leads
,
which leads 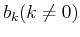 to be a fractional function of
to be a fractional function of 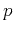 .
Differently from that, we use the following condition,
.
Differently from that, we use the following condition,
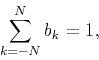 |
(27) |
where 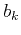 can be proved to be polynomials of
can be proved to be polynomials of 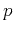 .
.
Let vector
![$\mathbf b=[b_0,b_N,\dots,b_1,b_{-1},\dots,b_{-N}]^\textrm T$](img120.png) .
Combining equations I-3 and I-4,
we rewrite them into the following matrix form:
.
Combining equations I-3 and I-4,
we rewrite them into the following matrix form:
The matrix on the left side, denoted as 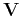 ,
can be split into four blocks
,
can be split into four blocks
![$\left[\begin{array}{c\vert c}
\tensor A & \tensor B \hline \tensor C & \tensor D
\end{array}\right]$](img123.png) as shown above.
Following the lemma of matrix inversion,
as shown above.
Following the lemma of matrix inversion,
![\begin{displaymath}
\tensor V^{-1}=\left[\begin{array}{cc}
(\tensor A-\tensor B\...
...\tensor C)^{-1}\tensor B\tensor D^{-1} \\
\end{array}\right],
\end{displaymath}](img124.png) |
(28) |
therefore the coefficients
![\begin{displaymath}
\mathbf b=\tensor V^{-1}[1,0,\dots,0]^\textrm T=
\left[\begi...
... A-\tensor B\tensor D^{-1}\tensor C)^{-1}
\end{array}\right].
\end{displaymath}](img125.png) |
(29) |
Let subindex
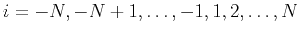 and
and 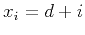 .
Submatrix
.
Submatrix 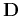 can be expressed as
can be expressed as
so
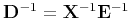 .
Denoting
.
Denoting
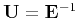 with elements
with elements
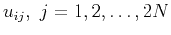 ,
as
,
as 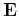 is a Vandermonde matrix,
is a Vandermonde matrix,
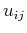 and Lagrange intepolating polynomials have the following relationship:
and Lagrange intepolating polynomials have the following relationship:
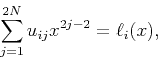 |
(30) |
where
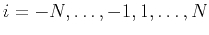 ,
and
,
and 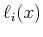 is the Lagrange polynomial related to the basis
is the Lagrange polynomial related to the basis 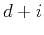 ,
,
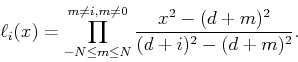 |
(31) |
Substituting the above equation, 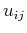 and
and 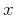 into equation I-7,
we can prove equation I-7.
It follows that
into equation I-7,
we can prove equation I-7.
It follows that
![\begin{displaymath}[\tensor E^{-1}\tensor C]_i=d\ell_i(d),
\end{displaymath}](img141.png) |
(32) |
![\begin{displaymath}[\tensor D^{-1}\tensor C]_i=
[\tensor X^{-1}\tensor E^{-1}\tensor C]_i=
\frac{d}{d+i}\ell_i(d),
\end{displaymath}](img142.png) |
(33) |
with
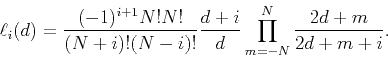 |
(34) |
Thus hence
and
![\begin{displaymath}[\tensor A-\tensor B\tensor D^{-1}\tensor C]^{-1} =
\frac{(2N)!(2N)!}{(4N)!N!N!}
\prod_{m=N+1}^{2N}(m^2-p^2).
\end{displaymath}](img147.png) |
(36) |
It is the coefficient 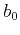 , a
, a 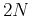 -th degree polynomial of
-th degree polynomial of 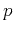 .
Substituting it into equation I-6,
the coefficients at
.
Substituting it into equation I-6,
the coefficients at
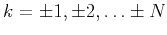 are expressed as
are expressed as
With the additional condition I-4 in 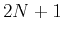 points approximation,
all the coefficients are polynomials of
points approximation,
all the coefficients are polynomials of 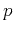 of
of 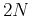 -th degree.
Thus the plane-wave destruction equation 6
therefore is proved to be a polynomial equation of
-th degree.
Thus the plane-wave destruction equation 6
therefore is proved to be a polynomial equation of 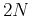 -th degree.
-th degree.
 |
 |
 |
 | Accelerated plane-wave destruction |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Chen, Fomel & Lu:
Previous: Acknowledgments
2013-03-02
![]() are polynomials of
are polynomials of ![]() ,
equation 4 is also a polynomial of
,
equation 4 is also a polynomial of ![]() ,
and the plane-wave destruction equation becomes
in turn a polynomial equation of
,
and the plane-wave destruction equation becomes
in turn a polynomial equation of ![]() .
The problem is to design a
.
The problem is to design a ![]() points filter
points filter ![]() with polynomial coefficients
such that the allpass system
with polynomial coefficients
such that the allpass system
![]() can approximate
the phase-shift operator
can approximate
the phase-shift operator
![]() .
Denoting the phase response of the system as
.
Denoting the phase response of the system as
![]() ,
that is
,
that is
![]() ,
the group delay of the system is
,
the group delay of the system is
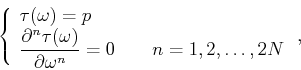
![]() from the above equations,
Thiran (1971) used an additional condition
from the above equations,
Thiran (1971) used an additional condition ![]() ,
which leads
,
which leads ![]() to be a fractional function of
to be a fractional function of ![]() .
Differently from that, we use the following condition,
.
Differently from that, we use the following condition,
![$\mathbf b=[b_0,b_N,\dots,b_1,b_{-1},\dots,b_{-N}]^\textrm T$](img120.png) .
Combining equations I-3 and I-4,
we rewrite them into the following matrix form:
.
Combining equations I-3 and I-4,
we rewrite them into the following matrix form:
![\begin{displaymath}
\left[\begin{array}{c\vert cccccc}
1 & 1 & \dots & 1 & 1 & \...
...begin{array}{c}
1 0 0 \vdots 0
\end{array}\right].
\end{displaymath}](img121.png)
![]() ,
can be split into four blocks
,
can be split into four blocks
![$\left[\begin{array}{c\vert c}
\tensor A & \tensor B \hline \tensor C & \tensor D
\end{array}\right]$](img123.png) as shown above.
Following the lemma of matrix inversion,
as shown above.
Following the lemma of matrix inversion,
![\begin{displaymath}
\tensor V^{-1}=\left[\begin{array}{cc}
(\tensor A-\tensor B\...
...\tensor C)^{-1}\tensor B\tensor D^{-1} \\
\end{array}\right],
\end{displaymath}](img124.png)
![]() and
and ![]() .
Submatrix
.
Submatrix ![]() can be expressed as
can be expressed as
![\begin{eqnarray*}
\tensor D &=& \tensor E\tensor X \\
&=&
\left[\begin{array}{c...
...} \vdots x_{-1} x_1 \vdots x_N
\end{array}\right],
\end{eqnarray*}](img129.png)
![]() and
and ![]() into equation I-7,
we can prove equation I-7.
It follows that
into equation I-7,
we can prove equation I-7.
It follows that
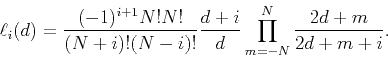
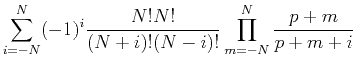
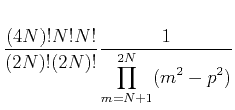
![\begin{displaymath}[\tensor A-\tensor B\tensor D^{-1}\tensor C]^{-1} =
\frac{(2N)!(2N)!}{(4N)!N!N!}
\prod_{m=N+1}^{2N}(m^2-p^2).
\end{displaymath}](img147.png)
![]() , a
, a ![]() -th degree polynomial of
-th degree polynomial of ![]() .
Substituting it into equation I-6,
the coefficients at
.
Substituting it into equation I-6,
the coefficients at
![]() are expressed as
are expressed as
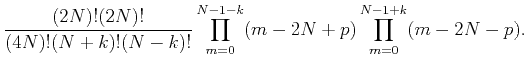
![]() points approximation,
all the coefficients are polynomials of
points approximation,
all the coefficients are polynomials of ![]() of
of ![]() -th degree.
Thus the plane-wave destruction equation 6
therefore is proved to be a polynomial equation of
-th degree.
Thus the plane-wave destruction equation 6
therefore is proved to be a polynomial equation of ![]() -th degree.
-th degree.