 |
 |
 |
 | Accelerated plane-wave destruction |  |
![[pdf]](icons/pdf.png) |
Next: Accelerated PWD
Up: Theory
Previous: Theory
The local plane wave can be represented by the following differential equation
(Claerbout, 1992):
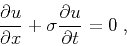 |
(1) |
where 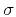 is the local slope in continuous space,
with dimension time/length.
The wavefields observed at the two positions
is the local slope in continuous space,
with dimension time/length.
The wavefields observed at the two positions 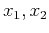 have a time delay
which is proportional to their distance,
have a time delay
which is proportional to their distance,
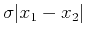 .
In the sampled system with space and time intervals
.
In the sampled system with space and time intervals 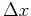 and
and 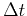 ,
we define the discrete space slope in the unit of
,
we define the discrete space slope in the unit of
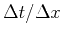 ,
as
,
as
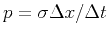 .
As
.
As 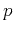 is independent of the sampling interval,
it can be directly used in irregular dataset
(in this case, the unit of the slopes becomes space variant).
The time delay between two adjacent positions is then the slope
is independent of the sampling interval,
it can be directly used in irregular dataset
(in this case, the unit of the slopes becomes space variant).
The time delay between two adjacent positions is then the slope 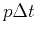 :
:
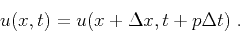 |
(2) |
With the  transform applied along both time and space directions,
the above equation becomes
transform applied along both time and space directions,
the above equation becomes
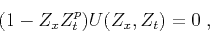 |
(3) |
where 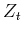 is the unit time-shift operator,
is the unit time-shift operator,
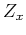 denotes the unit space-shift operator
and
denotes the unit space-shift operator
and 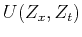 is the
is the 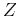 transform of
transform of 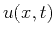 .
The operator
.
The operator 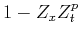 is the plane-wave destructor.
Using Thiran's fractional delay filter
is the plane-wave destructor.
Using Thiran's fractional delay filter
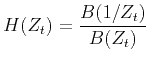 (Thiran, 1971)
to approximate the time-shift operator
(Thiran, 1971)
to approximate the time-shift operator
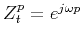 ,
where
,
where 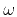 is the circular frequency,
the plane-wave destructor can be expressed as
(Fomel, 2002),
is the circular frequency,
the plane-wave destructor can be expressed as
(Fomel, 2002),
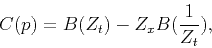 |
(4) |
where
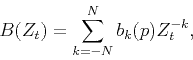 |
(5) |
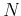 is the order of the noncausal temporal filter
and
is the order of the noncausal temporal filter
and 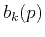 are functions of the local slope
are functions of the local slope 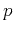 .
.
Equation 4 is a 2D filter.
Applying the filter at an arbitrary point in the wavefield,
the plane-wave destruction equation 3 becomes
a nonlinear equation for the local slope 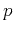 :
:
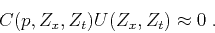 |
(6) |
An iterative method, such as Newton's method,
can be applied to find the slope.
In practice, wavefields are polluted by noise
and the plane wave assumption may not hold true
where faults and conflicting boundaries exist.
To obtain a stable slope estimation,
an additional smoothing regularization process (Fomel, 2007a)
is needed at each step.
The total computational cost of slope estimation by
plane-wave destruction becomes
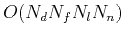 ,
where
,
where 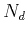 is the size of the data,
is the size of the data,
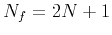 is the size of the filter,
is the size of the filter,
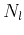 is the number of linear iterations for regularization,
and
is the number of linear iterations for regularization,
and 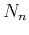 is the number of nonlinear iterations
for solving equation 6.
Typical values are
is the number of nonlinear iterations
for solving equation 6.
Typical values are  ,
, 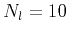 -50, and
-50, and 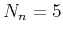 -10.
-10.
 |
 |
 |
 | Accelerated plane-wave destruction |  |
![[pdf]](icons/pdf.png) |
Next: Accelerated PWD
Up: Theory
Previous: Theory
2013-03-02
![]() transform applied along both time and space directions,
the above equation becomes
transform applied along both time and space directions,
the above equation becomes
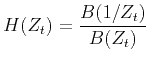 (Thiran, 1971)
to approximate the time-shift operator
(Thiran, 1971)
to approximate the time-shift operator
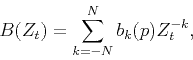
![]() :
:
![]() ,
where
,
where ![]() is the size of the data,
is the size of the data,
![]() is the size of the filter,
is the size of the filter,
![]() is the number of linear iterations for regularization,
and
is the number of linear iterations for regularization,
and ![]() is the number of nonlinear iterations
for solving equation 6.
Typical values are
is the number of nonlinear iterations
for solving equation 6.
Typical values are ![]() ,
, ![]() -50, and
-50, and ![]() -10.
-10.