 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Synthetic realizations
Up: Statistical model of heterogeneities
Previous: Statistical model of heterogeneities
Among different concepts introduced by the theory of fractals (Mandelbrot, 1983),
self-affine property accounts for invariance of roughness of a curve observed at different scales.
Self-affine fractals can be characterized by the power-law dependence of their energy spectrum 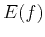 on frequency
on frequency 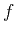 :
:
The exponent 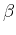 , in the energy spectrum
, in the energy spectrum
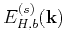 from equation 7, is
from equation 7, is
For 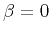 , energy spectrum is constant and describes the familiar white noise.
Causal integration of Gaussian white noise produces the classical Brownian motion, or random walk,
characteristic of diffusion processes, and results in an energy spectrum with
, energy spectrum is constant and describes the familiar white noise.
Causal integration of Gaussian white noise produces the classical Brownian motion, or random walk,
characteristic of diffusion processes, and results in an energy spectrum with 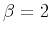 .
The autocorrelation function of Brownian motion signals is a decreasing exponential and
the autocorrelation in equation 6 properly reduces to
.
The autocorrelation function of Brownian motion signals is a decreasing exponential and
the autocorrelation in equation 6 properly reduces to ![$\exp{[-r/b]}$](img71.png) for
for 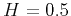 .
Another interesting form of spectrum is for
.
Another interesting form of spectrum is for 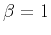 .
The associated signal is called Flicker noise (Schottky, 1926; Dolan et al., 1998) and can be interpreted
as the superposition of different relaxation processes.
For geological layers, such form of spectrum was interpreted as the expression
of quasi-cyclicity and blocky layering (Shtatland, 1991).
Generalization, including Gaussian white noise and Brownian motion, leads to two types
of fractal signals (Li, 2003; Shtatland, 1991; Turcotte, 1997), namely
.
The associated signal is called Flicker noise (Schottky, 1926; Dolan et al., 1998) and can be interpreted
as the superposition of different relaxation processes.
For geological layers, such form of spectrum was interpreted as the expression
of quasi-cyclicity and blocky layering (Shtatland, 1991).
Generalization, including Gaussian white noise and Brownian motion, leads to two types
of fractal signals (Li, 2003; Shtatland, 1991; Turcotte, 1997), namely
- fractional Gaussian noise (fGn) defined as filtered Gaussian white noise with
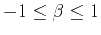 ,
,
- fractional Brownian motion (fBm) built by causal integration of fGn above and resulting in
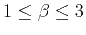 .
.
The fGn is stationary and Gaussian, whereas the fBm is neither stationary nor Gaussian.
Exponent 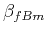 of the fBm is related to exponent
of the fBm is related to exponent 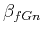 of the fGn, used for integration, by
of the fGn, used for integration, by
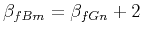 .
.
The significance of parameter 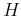 in equation 10 is delicate and connected to the Hurst exponent
in equation 10 is delicate and connected to the Hurst exponent 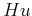 ,
which measures the correlation of time series (Hurst, 1951) by
,
which measures the correlation of time series (Hurst, 1951) by
where 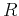 and
and 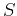 are respectively range of variations and variance
calculated for the length
are respectively range of variations and variance
calculated for the length 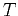 of the signal. The meaning of the value of
of the signal. The meaning of the value of 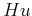 is
is
- antipersistence for
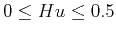 ,
,
- random process for
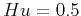 , and
, and
- persistence for
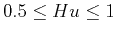 .
.
Estimation of 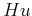 using formula 11 is relevant only for fGn signals (Turcotte, 1997).
For example, Gaussian white noise produces
using formula 11 is relevant only for fGn signals (Turcotte, 1997).
For example, Gaussian white noise produces 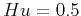 .
Parameter
.
Parameter 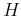 defined in equation 10 is associated with the Hurst exponent by
defined in equation 10 is associated with the Hurst exponent by
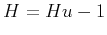 for fGn with
for fGn with
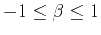 ;
;
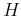 equals the Hurst exponent of incremented fGn (Li, 2003) for fBm with
equals the Hurst exponent of incremented fGn (Li, 2003) for fBm with
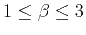 .
.
The different self-affine 1D fractal models are presented in Table 1
according to the nature and persistency of the signal.
A previous analysis of the logarithm of acoustic impedance from well data
by Walden and Hosken (1985) shows
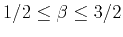 , promoting the so-called
, promoting the so-called 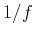 geology.
An improved solution, reproducing the complete well log sequence in sedimentary rocks, uses
a similar random process based on fractional Lévy motion (Painter and Paterson, 1994),
but fBm can be adequate at small scales, inside different facies (Lu et al., 2002).
geology.
An improved solution, reproducing the complete well log sequence in sedimentary rocks, uses
a similar random process based on fractional Lévy motion (Painter and Paterson, 1994),
but fBm can be adequate at small scales, inside different facies (Lu et al., 2002).
| Fractal exponent |
Von Kármán exponent 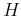 |
Description |
Geology |
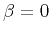 |
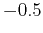 |
Gaussian white noise |
Random process |
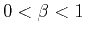 |
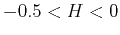 |
Persistent fGn |
|
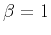 |
 |
Flicker noise |
Blocky layers |
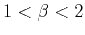 |
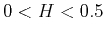 |
Antipersistent fBm |
Quasi-cyclic deposition |
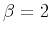 |
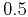 |
Brownian walk |
Random deposition |
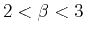 |
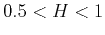 |
Persistent fBm |
Transitional deposition |
Table 1. Classification of 1D fractal statistics according to the exponent 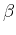 and geological interpretation.
and geological interpretation.
 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Synthetic realizations
Up: Statistical model of heterogeneities
Previous: Statistical model of heterogeneities
2013-03-02
![]() on frequency
on frequency ![]() :
:
![]() in equation 10 is delicate and connected to the Hurst exponent
in equation 10 is delicate and connected to the Hurst exponent ![]() ,
which measures the correlation of time series (Hurst, 1951) by
,
which measures the correlation of time series (Hurst, 1951) by