 |
 |
 |
 | Signal and noise separation in prestack seismic data using velocity-dependent seislet transform |  |
![[pdf]](icons/pdf.png) |
Next: Separation of primaries and
Up: Theory
Previous: VD-slope pattern for primary
In a laterally homogeneous model, the NMO equation 6
flattens primary events on a CMP gather with offset 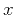 and time
and time 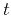 to its zero-offset traveltime
to its zero-offset traveltime 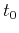 . Brown and Guitton (2005) use an analogous
NMO equation for pegleg multiples under locally 1D earth assumption. For
example, first-order pegleg can be kinematically approximated by
pseudo-primary with the same offset but with an additional zero-offset
traveltime
. Brown and Guitton (2005) use an analogous
NMO equation for pegleg multiples under locally 1D earth assumption. For
example, first-order pegleg can be kinematically approximated by
pseudo-primary with the same offset but with an additional zero-offset
traveltime 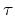 . The NMO equation for an
. The NMO equation for an 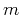 th-order pegleg multiple
is generalized to
th-order pegleg multiple
is generalized to
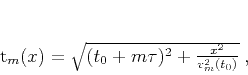 |
(8) |
where 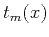 is the corresponding multiple traveltime recorded at
offset
is the corresponding multiple traveltime recorded at
offset 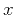 and the effective RMS velocity
and the effective RMS velocity 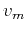 is
defined according to Dix's equation as:
is
defined according to Dix's equation as:
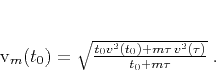 |
(9) |
In marine seismic data, 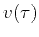 is constant water velocity, and
it assumes that we are able to pick zero-offset traveltime
is constant water velocity, and
it assumes that we are able to pick zero-offset traveltime
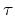 of the water bottom. According to the definition of slopes for
primaries (equation 7), slopes for pegleg multiples can be
calculated analogously by:
of the water bottom. According to the definition of slopes for
primaries (equation 7), slopes for pegleg multiples can be
calculated analogously by:
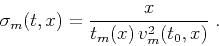 |
(10) |
Equation 10 provides the estimation of multiple slopes,
which we use to define VD-seislet frame for representing pegleg
multiples of different orders.
 |
 |
 |
 | Signal and noise separation in prestack seismic data using velocity-dependent seislet transform |  |
![[pdf]](icons/pdf.png) |
Next: Separation of primaries and
Up: Theory
Previous: VD-slope pattern for primary
2015-10-24
![]() and time
and time ![]() to its zero-offset traveltime
to its zero-offset traveltime ![]() . Brown and Guitton (2005) use an analogous
NMO equation for pegleg multiples under locally 1D earth assumption. For
example, first-order pegleg can be kinematically approximated by
pseudo-primary with the same offset but with an additional zero-offset
traveltime
. Brown and Guitton (2005) use an analogous
NMO equation for pegleg multiples under locally 1D earth assumption. For
example, first-order pegleg can be kinematically approximated by
pseudo-primary with the same offset but with an additional zero-offset
traveltime ![]() . The NMO equation for an
. The NMO equation for an ![]() th-order pegleg multiple
is generalized to
th-order pegleg multiple
is generalized to