Adaptive prediction filtering in $t$ -$x$ -$y$ domain for random noise attenuation using regularized nonstationary autoregression

3D space-noncausal adaptive prediction filtering

Equation 2 and 4 show space-forward prediction equations, which are similar as the causal prediction filtering equations in $f$ -$x$ domain (Gulunay, 2000). Furthermore, $t$ -$x$ prediction filter also includes time-noncausal coefficients. In the case of both space-forward and space-backward prediction equations (space-noncausal prediction filter), equation 4 can be written (Naghizadeh and Sacchi, 2009; Liu et al., 2012; Liu and Chen, 2013; Spitz, 1991) with the results averaged: 2pt

$$\tilde{B}_{i,j}(t,x) = \arg\min_{B_{i,j}(t,x)}\Vert S(t,x)- \sum_{j=-N,j\neq0}^{N} \sum_{i=-M}^{M} B_{i,j}(t,x)S_{i,j}(t,x)\Vert _2^2$$

$$+ \epsilon^2 \sum_{j=-N,j\neq0}^{N} \sum_{i=-M}^{M} \Vert\mathbf{R}[B_{i,j}(t,x)]\Vert _2^2\;,$$ (5)

Equation 5 shows that one sample in $t$ -$x$ domain can be predicted by the samples in adjacent traces with weight coefficients $B_{i,j}(t,x)$ , which is time- and space-varying. The equation assumes that the seismic data only consist of plane waves $\sum_{j=-N,j\neq0}^{N} \sum_{i=-M}^{M} B_{i,j}(t,x)S_{i,j}(t,x)$ and random noise that corresponds to a least-squares error.

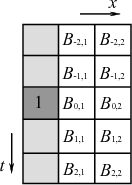
Figure 1a shows a 2D space-causal APF structure, which is time-noncausal filter. White grids stand for prediction samples and the dark-grey grid is the output (or target) position, while light-grey grids are unused samples. The filter size of the space-causal APF is $N\times(2M+1)$ . Meanwhile, space-noncausal APF (Figure 1b) has a symmetric structure along time and space axes. The filter size of the space-noncausal APF is $2N\times(2M+1)$ . The 3D $t$ -$x$ -$y$ APF also has space-causal or space-noncausal structure, Figure 2 shows the noncausal one. In a 3D seismic datacube, the plane events can be predicted along two different spatial directions. A 2D $t$ -$x$ APF will have difficulty preserving accurate plane waves because it only uses the information in $x$ or $y$ direction, however, a 3D $t$ -$x$ -$y$ APF provides a more natural structure. $t$ -$x$ -$y$ adaptive prediction filtering for random noise attenuation follows two steps:

1. Estimating 3D space-noncausal APF coefficients $\tilde{B}_{i,j,k}(t,x,y)$ by solving the regularized least-squares problem (equation 4 or 5 in 2D): 2pt

$$\tilde{B}_{i,j,k}(t,x,y) = \arg\min_{B_{i,j,k}(t,x,y)}\Vert S(t,x,y)- \sum_{k=-L,k\neq0}^{L... ..._{j=-N,j\neq0}^{N} \sum_{i=-M}^{M} B_{i,j,k}(t,x,y)S_{i,j,k}(t,x,y)\Vert _2^2$$

$$+ \epsilon^2 \sum_{k=-L,k\neq0}^{L} \sum_{j=-N,j\neq0}^{N} \sum_{i=-M}^{M} \Vert\mathbf{R}[B_{i,j,k}(t,x,y)]\Vert _2^2\;,$$ (6)

2. Calculating noise-free signal $\tilde{S}(t,x,y)$ according to 2pt

$$\tilde{S}(t,x,y) = \sum_{k=-L,k\neq0}^{L} \sum_{j=-N,j\neq0}^{N} \sum_{i=-M}^{M} \tilde{B}_{i,j,k}(t,x,y)S_{i,j,k}(t,x,y) \;,$$ (7)

causal2d,noncausal2d
Figure 1. Schematic illustration of a 2D $t$ -$x$ APF. A space-causal filter (a) and a space-noncausal filter (b).

noncausal3d
Figure 2. Schematic illustration of a 3D $t$ -$x$ -$y$ space-noncausal APF.

Adaptive prediction filtering in $t$ -$x$ -$y$ domain for random noise attenuation using regularized nonstationary autoregression