 |
 |
 |
 | Adaptive prediction filtering in 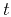 -
-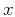 -
-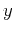 domain for random noise attenuation using regularized nonstationary autoregression
domain for random noise attenuation using regularized nonstationary autoregression |  |
![[pdf]](icons/pdf.png) |
Next: 3D space-noncausal adaptive prediction
Up: Theory
Previous: Theory
Consider a 2D prediction filter (general for stationary PF) with
ten prediction coefficients  :
:
 |
(1) |
where  is time shift,
is time shift,  is space shift, the vertical axis is time
axis, and the horizontal axis is space axis. The output position is
under the ``
is space shift, the vertical axis is time
axis, and the horizontal axis is space axis. The output position is
under the `` '' coefficient on the left side of filter and
``
'' coefficient on the left side of filter and
`` '' indicates time- and space-varying samples. The filter is
noncausal along the time axis and causal along the space axis. More
filter structures will be discussed later. The PF has the different
coefficients from PEF, which includes causal time prediction
coefficients.
'' indicates time- and space-varying samples. The filter is
noncausal along the time axis and causal along the space axis. More
filter structures will be discussed later. The PF has the different
coefficients from PEF, which includes causal time prediction
coefficients.
To obtain stationary PF coefficients, one can solve the
over-determined least-squares problem
2pt
where
 represents the translation of linear events
represents the translation of linear events
 in both time and space directions with time shift
in both time and space directions with time shift  and
space shift
and
space shift  . The choice of the filter size depends on the maximum
dip of the plane waves in the data and the number of dips. For
nonlinear events, cutting data into overlapping windows (patching) is
a common method to handle nonstationarity
(Claerbout, 2010), although it occasionally fails in the presence
of variable dips.
. The choice of the filter size depends on the maximum
dip of the plane waves in the data and the number of dips. For
nonlinear events, cutting data into overlapping windows (patching) is
a common method to handle nonstationarity
(Claerbout, 2010), although it occasionally fails in the presence
of variable dips.
For nonstationary situations, we can also assume local linearization
of the data. For estimating APF coefficients, nonstationary
autoregression allows the coefficients  to change with both
to change with both
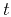 and
and 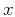 . The new adaptive filter can be designed as
. The new adaptive filter can be designed as
 |
(3) |
In the linear notation, prediction coefficients
 can be
obtained by solving the under-determined least-squares problem
2pt
can be
obtained by solving the under-determined least-squares problem
2pt
where
 is the regularization operator and
is the regularization operator and  is a
scalar regularization parameter. This approach was described by
Fomel (2009) as regularized nonstationary autoregression (RNA). Shaping
regularization (Fomel, 2007) specified a shaping (smoothing)
operator
is a
scalar regularization parameter. This approach was described by
Fomel (2009) as regularized nonstationary autoregression (RNA). Shaping
regularization (Fomel, 2007) specified a shaping (smoothing)
operator
 instead of
instead of
 and provided better
numerical properties than Tikhonov's regularization
(Tikhonov, 1963) in equation 4. The advantages of
the shaping regularization include an intuitive selection of
regularization parameters and fast iteration convergence. Coefficients
and provided better
numerical properties than Tikhonov's regularization
(Tikhonov, 1963) in equation 4. The advantages of
the shaping regularization include an intuitive selection of
regularization parameters and fast iteration convergence. Coefficients
 get constrained by regularization. The required
parameters are the size and shape of the filter,
get constrained by regularization. The required
parameters are the size and shape of the filter,
 , and
the smoothing radius for shaping regularization. The size of APF
controls the range and the number of the predicted dips. Larger filter
parameters,
, and
the smoothing radius for shaping regularization. The size of APF
controls the range and the number of the predicted dips. Larger filter
parameters,  and
and  , are able to predict more accurate dips,
however, the APFs with the large filter size pass more random noise
and add more computational cost. As the smoothing radius of the APF
increases, the APF removes not only more random noise but also some
structural details. The APF is able to be extended to the adaptive PEF
(APEF), which shows a expected representation of nonstationary signal
and is fit for seismic data interpolation (Liu and Fomel, 2011) and random
noise attenuation (Liu and Liu, 2011). However, the structure of APEF is
different from that of APF, which excludes the causal time prediction
coefficients and forces only lateral predictions. Meanwhile, in this
paper, we use a two-step method that estimates APF coefficients by
solving an under-determined problem and calculates noise-free signal.
The proposed method is different from the two-step APEF denoising
including APEF estimation for signal and noise plus signal and noise
separation by solving a least-square system as shown in
Liu and Liu (2011).
, are able to predict more accurate dips,
however, the APFs with the large filter size pass more random noise
and add more computational cost. As the smoothing radius of the APF
increases, the APF removes not only more random noise but also some
structural details. The APF is able to be extended to the adaptive PEF
(APEF), which shows a expected representation of nonstationary signal
and is fit for seismic data interpolation (Liu and Fomel, 2011) and random
noise attenuation (Liu and Liu, 2011). However, the structure of APEF is
different from that of APF, which excludes the causal time prediction
coefficients and forces only lateral predictions. Meanwhile, in this
paper, we use a two-step method that estimates APF coefficients by
solving an under-determined problem and calculates noise-free signal.
The proposed method is different from the two-step APEF denoising
including APEF estimation for signal and noise plus signal and noise
separation by solving a least-square system as shown in
Liu and Liu (2011).
 |
 |
 |
 | Adaptive prediction filtering in 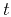 -
-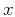 -
-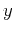 domain for random noise attenuation using regularized nonstationary autoregression
domain for random noise attenuation using regularized nonstationary autoregression |  |
![[pdf]](icons/pdf.png) |
Next: 3D space-noncausal adaptive prediction
Up: Theory
Previous: Theory
2014-12-07
![]() :
:
![]() to change with both
to change with both
![]() and
and ![]() . The new adaptive filter can be designed as
. The new adaptive filter can be designed as
![]() can be
obtained by solving the under-determined least-squares problem
2pt
can be
obtained by solving the under-determined least-squares problem
2pt