Next: INTERVAL VELOCITY
Up: OPPORTUNITIES FOR SMART DIRECTIONS
Previous: The meaning of the
It is important to use regularization to solve many examples.
It is important to precondition,
because in practice,
computer power is often a limiting factor.
It is important to be able to begin from a nonzero starting solution,
because in nonlinear problems we must restart from an earlier solution.
Putting all three requirements together leads to a little problem.
It turns out the three together lead us to needing
a preconditioning transformation that is invertible.
Let us see why this is so.
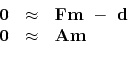 |
(28) |
First,
we change variables from 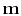 to
to
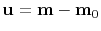 .
Clearly,
.
Clearly,
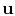 starts from
starts from
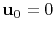 , and
, and
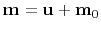 .
Then,
our regression pair becomes:
.
Then,
our regression pair becomes:
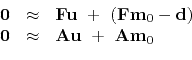 |
(29) |
This result differs from the original regression in only two minor ways,
(1) revised data, and (2) a little more general form of the regularization,
the extra term
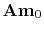 .
.
Now,
let us introduce preconditioning.
From the regularization,
we see preconditioning introduces the preconditioning variable
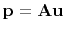 .
Our regression pair becomes:
.
Our regression pair becomes:
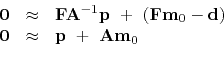 |
(30) |
Here is the problem:
We now require both 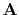 and
and
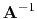 operators.
In 2- and 3-dimensional spaces, we do not know very many operators
with an easy inverse.
That reason is why I found myself pushed to come up with the helix methodology
of Chapter
operators.
In 2- and 3-dimensional spaces, we do not know very many operators
with an easy inverse.
That reason is why I found myself pushed to come up with the helix methodology
of Chapter ![[*]](icons/crossref.png) --because it provides invertible operators for
smoothing and roughening.
--because it provides invertible operators for
smoothing and roughening.
Next: INTERVAL VELOCITY
Up: OPPORTUNITIES FOR SMART DIRECTIONS
Previous: The meaning of the
2015-05-07
![]() .
Our regression pair becomes:
.
Our regression pair becomes: