 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: Smoothing the denominator spectrum
Up: UNIVARIATE LEAST SQUARES
Previous: Dividing by zero smoothly
Another way to say 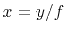 is to say
is to say 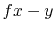 is small, or
is small, or 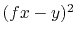 is small.
This does not solve the problem of
is small.
This does not solve the problem of 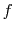 going to zero,
so we need the idea that
going to zero,
so we need the idea that 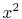 does not get too big.
To find
does not get too big.
To find 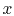 , we minimize the quadratic function in
, we minimize the quadratic function in 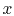 .
.
 |
(2) |
The second term is called a ``damping factor,''
because it prevents 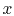 from going to
from going to 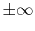 when
when
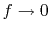 .
Set
.
Set 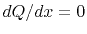 , which gives:
, which gives:
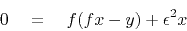 |
(3) |
Equation (3) yields our earlier common-sense guess
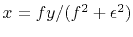 .
It also leads us to wider areas of application in which the elements are complex
vectors and matrices.
.
It also leads us to wider areas of application in which the elements are complex
vectors and matrices.
With Fourier transforms,
the signal 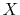 is a complex number at each frequency
is a complex number at each frequency 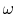 .
Therefore we generalize equation (2) to:
.
Therefore we generalize equation (2) to:
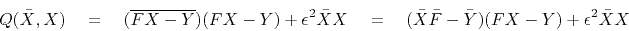 |
(4) |
To minimize 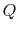 , we could use a real-values approach,
where we express
, we could use a real-values approach,
where we express
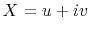 in terms of two real values
in terms of two real values 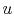 and
and 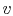 ,
and then set
,
and then set
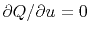 and
and
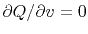 .
The approach we take, however,
is to use complex values,
where we set
.
The approach we take, however,
is to use complex values,
where we set
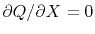 and
and
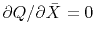 .
Let us examine
.
Let us examine
 :
:
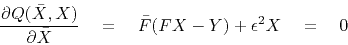 |
(5) |
The derivative
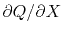 is
the complex conjugate of
is
the complex conjugate of
 .
Therefore, if either is zero, the other is also zero.
Thus, we do not need to specify both
.
Therefore, if either is zero, the other is also zero.
Thus, we do not need to specify both
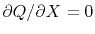 and
and
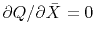 .
I usually set
.
I usually set
 equal to zero.
Solving equation (5) for
equal to zero.
Solving equation (5) for 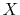 gives equation (1).
gives equation (1).
Equation (1) solves  for
for 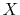 ,
giving the solution for what is called
``the deconvolution problem with a known wavelet
,
giving the solution for what is called
``the deconvolution problem with a known wavelet  .''
Analogously, we can use
.''
Analogously, we can use  when the filter
when the filter  is unknown,
but the input
is unknown,
but the input 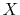 and output
and output 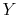 are given.
Simply interchange
are given.
Simply interchange 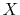 and
and  in the derivation and result.
in the derivation and result.
 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: Smoothing the denominator spectrum
Up: UNIVARIATE LEAST SQUARES
Previous: Dividing by zero smoothly
2014-12-01
![]() is a complex number at each frequency
is a complex number at each frequency ![]() .
Therefore we generalize equation (2) to:
.
Therefore we generalize equation (2) to:
![]() for
for ![]() ,
giving the solution for what is called
``the deconvolution problem with a known wavelet
,
giving the solution for what is called
``the deconvolution problem with a known wavelet ![]() .''
Analogously, we can use
.''
Analogously, we can use ![]() when the filter
when the filter ![]() is unknown,
but the input
is unknown,
but the input ![]() and output
and output ![]() are given.
Simply interchange
are given.
Simply interchange ![]() and
and ![]() in the derivation and result.
in the derivation and result.