 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: KRYLOV SUBSPACE ITERATIVE METHODS
Up: From the frequency domain
Previous: Unknown filter
For solving the unknown-input problem,
we put the known filter 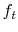 in a matrix of downshifted columns
in a matrix of downshifted columns 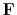 .
Our statement of wishes is now to find
.
Our statement of wishes is now to find 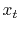 so that
so that
 .
We can expect to have trouble finding unknown inputs
.
We can expect to have trouble finding unknown inputs 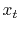 when we are dealing with certain kinds of filters,
such as bandpass filters.
If the output is zero in a frequency band,
we are never able to find the input in that band
and need to prevent
when we are dealing with certain kinds of filters,
such as bandpass filters.
If the output is zero in a frequency band,
we are never able to find the input in that band
and need to prevent 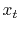 from diverging there.
We prevent divergence by the statement that we wish
from diverging there.
We prevent divergence by the statement that we wish
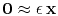 ,
where
,
where 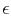 is a parameter that is small
with exact size chosen by experimentation.
Putting both wishes into a single, partitioned matrix equation gives:
is a parameter that is small
with exact size chosen by experimentation.
Putting both wishes into a single, partitioned matrix equation gives:
![\begin{displaymath}
\left[
\begin{array}{c}
\bold 0 \\
\bold 0
\end{array...
...
\begin{array}{c}
\bold y \\
\bold 0
\end{array} \right]
\end{displaymath}](img196.png) |
(48) |
To minimize the residuals 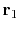 and
and 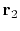 ,
we can minimize the scalar
,
we can minimize the scalar
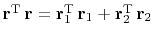 .
Expanding:
.
Expanding:
We solved this minimization
in the frequency domain
(beginning from equation (4)).
Formally the solution is found just as with equation (46),
but this solution looks unappealing in practice
because there are so many unknowns and
the problem can be solved much more quickly
in the Fourier domain.
To motivate ourselves to solve this problem in the time domain,
we need either to find an approximate solution method that is
much faster, or find ourselves with an application
that needs boundaries,
or needs time-variable weighting functions.
 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: KRYLOV SUBSPACE ITERATIVE METHODS
Up: From the frequency domain
Previous: Unknown filter
2014-12-01
![\begin{displaymath}
\left[
\begin{array}{c}
\bold 0 \\
\bold 0
\end{array...
...
\begin{array}{c}
\bold y \\
\bold 0
\end{array} \right]
\end{displaymath}](img196.png)