|
|
|
|
Regularization is model styling |
|
|---|
|
locfil
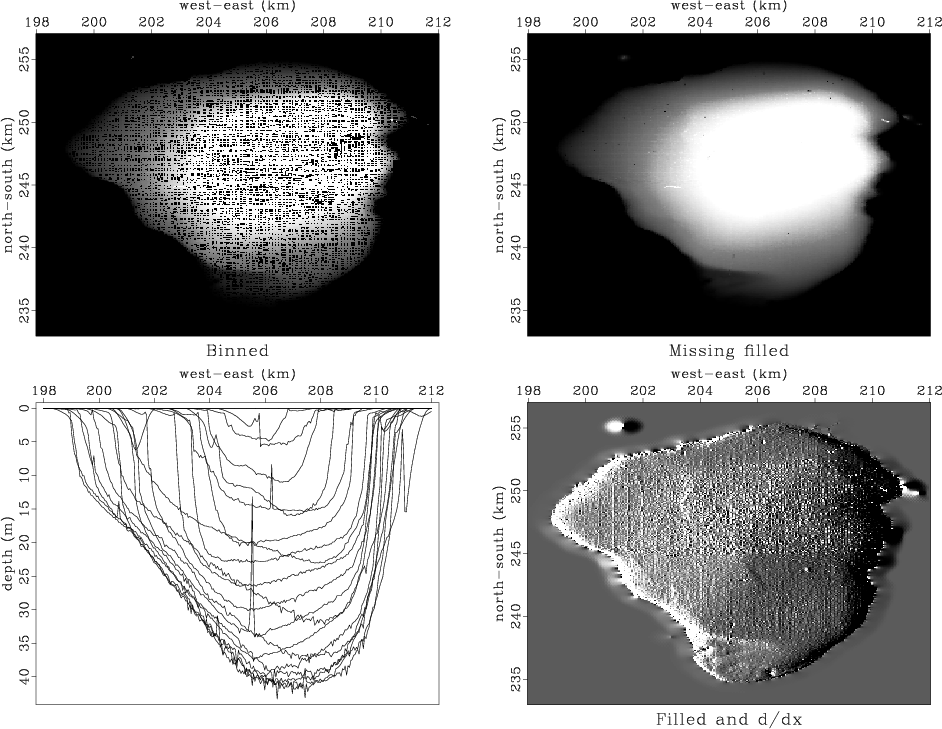
Figure 10. Views of the bottom of the Sea of Galilee. |
|
|
The first frame in Figure 10 shows simple binning.
A coarser mesh would avoid the empty bins but lose resolution.
As we refine the mesh for more detail,
the number of empty bins grows,
as does the care needed in devising a technique
for filling them.
This first frame uses the simple idea from Chapter ![]() of
spraying all the data values to the nearest bin
with bin2()
and dividing by the number in the bin.
Bins with no data obviously need to be filled in some other way.
I used a missing data program like that in the recent section
on ``wells not matching the seismic map.''
Instead of roughening with a Laplacian, however,
I used the gradient operator igrad2.
The solver is grad2fill().
of
spraying all the data values to the nearest bin
with bin2()
and dividing by the number in the bin.
Bins with no data obviously need to be filled in some other way.
I used a missing data program like that in the recent section
on ``wells not matching the seismic map.''
Instead of roughening with a Laplacian, however,
I used the gradient operator igrad2.
The solver is grad2fill().
for (i2=0; i2 < n2-1; i2++) {
for (i1=0; i1 < n1-1; i1++) {
i = i1+i2*n1;
if (adj) {
p[i+1] += r[i];
p[i+n1] += r[i+n12];
p[i] -= (r[i] + r[i+n12]);
} else {
r[i] += (p[i+1] - p[i]);
r[i+n12] += (p[i+n1] - p[i]);
}
}
}
|
void sf_grad2fill(int niter /* number of iterations */,
float* mm /* estimated model */,
bool *known /* mask */)
/*< Run optimization >*/
{
sf_solver (sf_igrad2_lop, sf_cgstep, n12, 2*n12, mm, zero,
niter, "x0", mm, "known", known, "end");
sf_cgstep_close ();
}
|
The output of the roughening operator is an image, a filtered version of the depth, a filtered version of something real. Such filtering can enhance the appearance of interesting features. For example, in scanning the shoreline of the roughened image (after missing data was filled), we see several ancient shorelines, now submerged. The roughened map is often more informative than the map.
The views expose several defects of the data acquisition and of our data processing. The impulsive glitches (St. Peter's fish?) need to be removed; but we must be careful not to throw out the sunken ships along with the bad data points. Even our best image shows clear evidence of the recording vessel's tracks. Strangely, some tracks are deeper than others. Perhaps the survey is assembled from work done in different seasons, and the water level varied by season. Perhaps, some days the vessel was more heavily loaded and the depth sounder was on a deeper keel. As for the navigation equipment, we can see that some data values are reported outside the lake!
We want the sharpest possible view of this classical site. A treasure hunt is never easy and no one guarantees we can find anything of great value; but at least the exercise is a good warm-up for submarine petroleum exploration.
|
|
|
|
Regularization is model styling |