An article A Perfect Storm: The Record of a Revolution by Eric-Jan Wagenmakers, a mathematical psychologist from the Unversity of Amsterdam, describes a reproducibility revolution, which is taking place in psychology:
An article A Perfect Storm: The Record of a Revolution by Eric-Jan Wagenmakers, a mathematical psychologist from the Unversity of Amsterdam, describes a reproducibility revolution, which is taking place in psychology:
The dynamics of political revolutions are in some ways similar to the academic revolution that has recently gripped the field of psychology. Over the last two decades, increasing levels of competition for scarce research funding have created a working environment that rewards productivity over reproducibility; this perverse incentive structure has caused some of the findings in the psychological literature to be spectacular and counter-intuitive, but likely false […] The general dissatisfaction with the state of the field was expressed in print only occasionally, until in 2011 two major events ignited the scientific revolution that is still in full force today.
The article was published this month by the Inquisitive Mind (In-Mind) magazine.
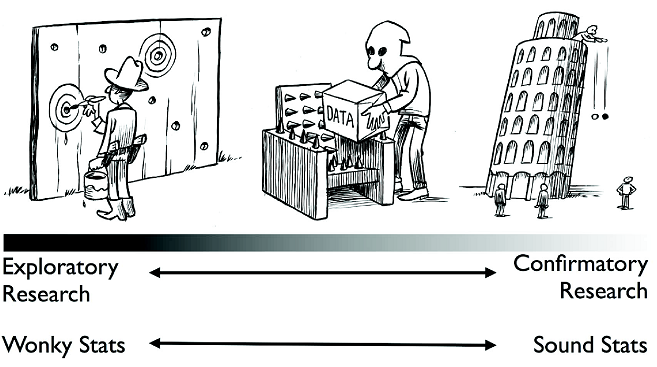
Eric-Jan concludes:
Although some researchers are less enthusiastic about the “replicability movement” than others, it is my prediction that the movement will grow until its impact is felt in other empirical disciplines including the neurosciences, biology, economy, and medicine. The problems that confront psychology are in no way unique, and this affords an opportunity to lead the way and create dependable guidelines on how to do research well. Such guidelines have tremendous value, both to individual scientists and to society as a whole.