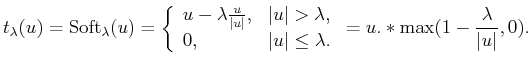|
 |
 |
 | Seislet-based morphological component analysis using scale-dependent exponential shrinkage |  |
![[pdf]](icons/pdf.png) |
Next: Understanding iterative thresholding as
Up: MCA with scale-dependent shaping
Previous: MCA with scale-dependent shaping
A general inverse problem combined with a priori constraint  can be written as an optimization problem
can be written as an optimization problem
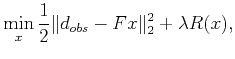 |
(1) |
where  is the model to be inverted, and
is the model to be inverted, and 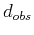 is the observations. To solve the problem with sparsity constraint
is the observations. To solve the problem with sparsity constraint
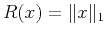 , the iterative shrinkage-thresholding (IST) algorithm has been proposed (Daubechies et al., 2004), which can be generally formulated as
, the iterative shrinkage-thresholding (IST) algorithm has been proposed (Daubechies et al., 2004), which can be generally formulated as
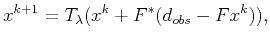 |
(2) |
where 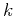 denotes the iteration number; and
denotes the iteration number; and 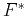 indicates the adjoint of
indicates the adjoint of 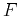 .
.
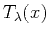 is an element-wise shrinkage operator with threshold
is an element-wise shrinkage operator with threshold 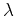 :
:
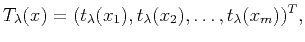 |
(3) |
in which the soft thresholding function (Donoho, 1995) is
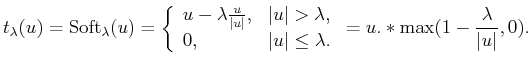 |
(4) |
Allowing for the missing elements in the data, the observations are connected to the complete data via the relation
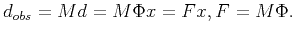 |
(5) |
where 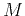 is an acquisition mask indicating the observed and missing values. Assume
is an acquisition mask indicating the observed and missing values. Assume 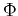 is a tight frame such that
is a tight frame such that
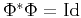 ,
,
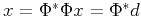 . It leads to
. It leads to
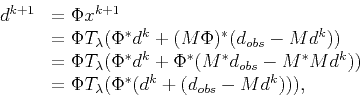 |
(6) |
in which we use
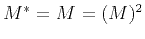 and
and
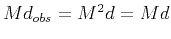 . Now we define a residual term as
. Now we define a residual term as
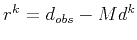 , thus Eq. (6) results in
, thus Eq. (6) results in
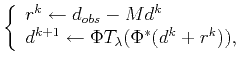 |
(7) |
which is equivalent to solving
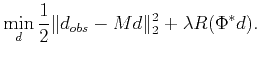 |
(8) |
Note that Eq. (8) analyzes the target unknown 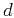 directly, without resort to
directly, without resort to 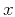 and
and 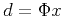 . Eq. (6) is referred to as the analysis formula (Elad et al., 2007). In this paper, we used the analysis formula because it directly addresses the problem in the data domain for the convenience of interpolation and signal separation.
. Eq. (6) is referred to as the analysis formula (Elad et al., 2007). In this paper, we used the analysis formula because it directly addresses the problem in the data domain for the convenience of interpolation and signal separation.
 |
 |
 |
 | Seislet-based morphological component analysis using scale-dependent exponential shrinkage |  |
![[pdf]](icons/pdf.png) |
Next: Understanding iterative thresholding as
Up: MCA with scale-dependent shaping
Previous: MCA with scale-dependent shaping
2021-08-31
![]() can be written as an optimization problem
can be written as an optimization problem