 |
 |
 |
 | RTM using effective boundary saving: A staggered grid GPU implementation |  |
![[pdf]](icons/pdf.png) |
Next: Storage analysis
Up: Effective boundary saving
Previous: Effective boundary for regular
The limitation of boundary saving strategy proposed in Dussaud et al. (2008) is that only regular grid finite difference scheme is considered in RTM. In the case of staggered grid, half grid points are employed to obtain higher accuracy for finite difference. Recursion from time 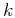 to
to 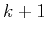 (or
(or 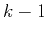 ) may not be realized with ease due to the Laplacian operator, which involves the second derivative. An effective approach is to split Eq. (1) into several first derivative equations or combinations of first derivative and second derivative equations. The first derivative is defined as
) may not be realized with ease due to the Laplacian operator, which involves the second derivative. An effective approach is to split Eq. (1) into several first derivative equations or combinations of first derivative and second derivative equations. The first derivative is defined as
![$\displaystyle \partial_u f=\frac{1}{\Delta u}\left( \sum_{i=1}^{N} c_i(f[u+i\Delta u/2]-f[u-i\Delta u/2])\right), u=z,x$](img81.png) |
(7) |
where the finite difference coefficients are listed in Table 2.
Table 2:
Finite difference coefficients for staggered grid (Order-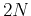 )
)
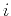
|
1 |
2 |
3 |
4 |
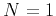
|
1 |
|
|
|
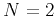
|
1.125 |
-0.0416667 |
|
|
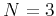
|
1.171875 |
-0.0651041667 |
0.0046875 |
|
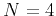
|
1.1962890625 |
-0.079752604167 |
0.0095703125 |
-0.000697544642857 |
The use of half grid points in staggered grid makes the effective boundary a little different from that in regular grid. To begin with, we define some intermediate auxiliary variables:
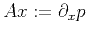 ,
,
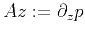 ,
,
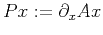 and
and
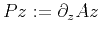 . Thus the acoustic wave equation reads
. Thus the acoustic wave equation reads
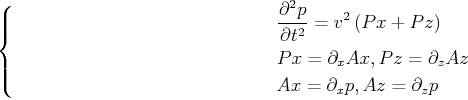 |
(8) |
It implies that we have to conduct 2 finite difference steps (one for 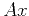 and
and 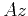 and the other for
and the other for 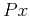 and
and 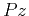 ) to compute the Laplacian in one step of time marching. Take 8-th order (
) to compute the Laplacian in one step of time marching. Take 8-th order (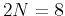 ) finite difference in
) finite difference in 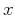 dimension for example. As can be seen from Figure 4, computing
dimension for example. As can be seen from Figure 4, computing
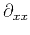 at
at 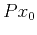 needs the correct values at
needs the correct values at 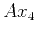 ,
,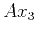 ,
,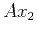 ,
,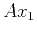 in the boundary; computing
in the boundary; computing 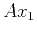 ,
,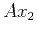 ,
,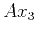 ,
,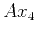 needs the correct values at
needs the correct values at 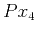 ,
, ,
, ,
,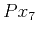 in the boundary. An intuitive approach is saving
in the boundary. An intuitive approach is saving 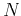 points of
points of 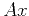 (
(
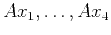 ) and
) and 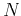 points of
points of 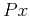 (
(
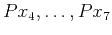 ). The saving procedure guarantees the correctness of these points in the wavefield. Another possible approach is just saving the
). The saving procedure guarantees the correctness of these points in the wavefield. Another possible approach is just saving the 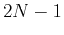 points of
points of 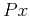 (
(
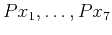 ). In this way, the values of
). In this way, the values of
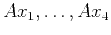 can be correctly obtained from the calculation of the first derivative.
The latter method is preferable because it is much easier for implementation while requiring less points. Speaking two dimensionally, some points in the four corners at in
can be correctly obtained from the calculation of the first derivative.
The latter method is preferable because it is much easier for implementation while requiring less points. Speaking two dimensionally, some points in the four corners at in
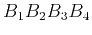 of Figure 1 may be still necessary to store, as shown in Figure 5a. The reason is that you are working with Laplacian, not second derivative in one dimension. Again, we switch our boundary saving part from out of
of Figure 1 may be still necessary to store, as shown in Figure 5a. The reason is that you are working with Laplacian, not second derivative in one dimension. Again, we switch our boundary saving part from out of
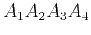 to
to
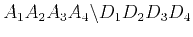 . Less grid points are required to guarantee correct reconstruction while points in the corner are no longer needed. Therefore, the proposed effective boundary for staggered finite difference needs
. Less grid points are required to guarantee correct reconstruction while points in the corner are no longer needed. Therefore, the proposed effective boundary for staggered finite difference needs 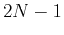 points to be saved on each side, see Figure 5b.
points to be saved on each side, see Figure 5b.

|
|---|
fig4
Figure 4. 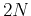 -th order staggered grid finite difference: correct backward propagation needs
-th order staggered grid finite difference: correct backward propagation needs 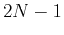 points on one side. For
points on one side. For 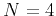 , computing
, computing
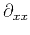 at
at 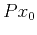 needs the correct values at
needs the correct values at 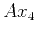 ,
, 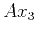 ,
, 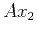 ,
, 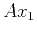 in the boundary; computing
in the boundary; computing 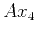 ,
,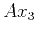 ,
, 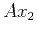 ,
, 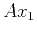 needs the correct values at
needs the correct values at 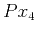 ,
,  ,
,  ,
, 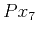 in the boundary. Thus,
in the boundary. Thus, 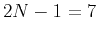 points in boundary zone is required to guarantee the correctness of the inner wavefield.
points in boundary zone is required to guarantee the correctness of the inner wavefield.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|

|
|---|
fig5
Figure 5. A 2-D sketch of required points for boundary saving for staggered grid finite difference: (a) Saving the points outside the model (red region). (b) Effective boundary, saving the points inside the model zone (gray region).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
 |
 |
 |
 | RTM using effective boundary saving: A staggered grid GPU implementation |  |
![[pdf]](icons/pdf.png) |
Next: Storage analysis
Up: Effective boundary saving
Previous: Effective boundary for regular
2021-08-31
![]() to
to ![]() (or
(or ![]() ) may not be realized with ease due to the Laplacian operator, which involves the second derivative. An effective approach is to split Eq. (1) into several first derivative equations or combinations of first derivative and second derivative equations. The first derivative is defined as
) may not be realized with ease due to the Laplacian operator, which involves the second derivative. An effective approach is to split Eq. (1) into several first derivative equations or combinations of first derivative and second derivative equations. The first derivative is defined as
![$\displaystyle \partial_u f=\frac{1}{\Delta u}\left( \sum_{i=1}^{N} c_i(f[u+i\Delta u/2]-f[u-i\Delta u/2])\right), u=z,x$](img81.png)
![]() ,
,
![]() ,
,
![]() and
and
![]() . Thus the acoustic wave equation reads
. Thus the acoustic wave equation reads

