|
|
|
|
Simulating propagation of separated wave modes in general anisotropic media, Part II: qS-wave propagators |
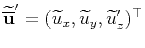 is defined by
is defined by
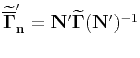 .
.
For a locally smooth medium, applying an inverse Fourier transformation to equation 24, we obtain another coupled forth-order linear system:
Due to the symmetry property of a VTI material, we may sum the horizontal components and replace the vertical component with the relation given in equation 27, and finally obtain a simpler second-order system that honors the kinematics of both qP- and qSV-waves:
For a 2-D VTI medium, equation 28 reduces to the following form:
If we apply the isotropic assumption by setting
![]() and
and
![]() ,
and sum the two equations in equation 28, we get the scalar wave equation:
,
and sum the two equations in equation 28, we get the scalar wave equation:
| (31) |
The derived pseudo-pure-mode qSV-wave equations have some interesting and valuable features.
First, the projection using matrix
![]() yields wave-mode separation to some
extent, because the chosen projection direction,
yields wave-mode separation to some
extent, because the chosen projection direction,
![]() , represents the polarization direction of
the SV-wave in an isotropic medium.
As investigated by Tsvankin and Chesnokov (1990) and Psencik and Gajewski (1998), and also demonstrated in Figure 1b,
the difference in polarization directions between isotropic and VTI media is
generally quite small in most propagation directions for SV-waves.
Therefore, considering the mode separator (namely equation 9) and the small projection deviation,
summing all the pseudo-pure-mode wavefield components in equation 28 or 30
partially achieves wave-mode separation and produces a scalar wavefield dominated by
the energy of qSV-waves. This will be demonstrated in the numerical examples.
Second, the pseudo-pure-mode wave equations are easier to calculate
than the original elastic wave equation because they have no terms of mixed partial
derivatives. More importantly, the summation of the horizontal components further simplifies the
wave equations and reduces the number of parameters needed for scalar qSV-wave extrapolation.
These features are undoubtedly useful for performing multicomponent seismic imaging and
inversion that mainly use wavefield kinematics when it is necessary to include anisotropy.
, represents the polarization direction of
the SV-wave in an isotropic medium.
As investigated by Tsvankin and Chesnokov (1990) and Psencik and Gajewski (1998), and also demonstrated in Figure 1b,
the difference in polarization directions between isotropic and VTI media is
generally quite small in most propagation directions for SV-waves.
Therefore, considering the mode separator (namely equation 9) and the small projection deviation,
summing all the pseudo-pure-mode wavefield components in equation 28 or 30
partially achieves wave-mode separation and produces a scalar wavefield dominated by
the energy of qSV-waves. This will be demonstrated in the numerical examples.
Second, the pseudo-pure-mode wave equations are easier to calculate
than the original elastic wave equation because they have no terms of mixed partial
derivatives. More importantly, the summation of the horizontal components further simplifies the
wave equations and reduces the number of parameters needed for scalar qSV-wave extrapolation.
These features are undoubtedly useful for performing multicomponent seismic imaging and
inversion that mainly use wavefield kinematics when it is necessary to include anisotropy.
|
|
|
|
Simulating propagation of separated wave modes in general anisotropic media, Part II: qS-wave propagators |